20．解方程组：$\left\{\begin{array}{l}{2x^2-3xy+y^2-4x-3y-3=0①}\\{2x-3y=1②}\end{array}\right.$．

19．如图，等腰梯形ABCD中，AD∥BC，AC，BD交于点O，下列结论错误的是（　　）

A．

△ABO≌△DCO

B．

AO=DO

C．

AC=DB

D．

BD平分∠ABC

18．已知菱形ABCD的周长为8，内角∠B=60°，则菱形ABCD的面积等于2$\sqrt{3}$．

17．如图1，AB是⊙O的直径，点C在⊙O上，且点C为弧BE的中点，连接AE并延长交BC延长线于点D．
（1）判断△ABD的形状，并说明理由；
（2）过点C作CM⊥AD，垂足为点F，如图2．
①求证：CF是⊙O的切线；
②若⊙O的半径为3，DF=1，求sinB的值．

16．假期里，小红和小慧去买菜，三次购买的西红柿价格和数量如下表：

单价/（元/千克）	4	3	2	合计
小红购买的数量/千克	1	2	3	6
小慧购买的数量/千克	2	2	2	6

（1）小红和小慧购买西红柿数量的中位数是2，众数是2；
（2）从平均价格看，谁买的西红柿要便宜些．
小亮的说法

每次购买单价相同，购买总量也相同，平均价格应该也一样，都是（4+3+2）÷3=3（元/千克），所以两人购买的西红柿一样便宜．

小明的说法

购买的总量虽然相同，但小红花了16元，小慧花了18元，平均价格不一样，所以购买的西红柿便宜

思考小亮和小明的说法，你认为谁说得对？为什么？
（3）小明在直角坐标系中画出反比例函数的图象，图象经过点P（如图），点P的横、纵坐标分别为小红和小慧购买西红柿价格的平均数．
①求此反比例函数的关系式；
②判断点Q（2，5）是否在此函数图象上．

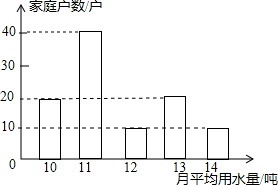15．某市自来水公司对某小区500户家庭的用水情况作一次调查，随机抽查了小区100户家庭一年的越平均用水量（单位：吨），并将调查结果绘制成如图所示的条形图）
（1）求这100个样本数据的平均数、众数和中位数；
（2）根据样本数据估计小区500户家庭中月平均用水量不超过12吨的约有多少用户？

14．如图，在△ABC中，DE∥BC，EC=2AE，BD=6，则AD=3．

13．（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．求证：CE=CF；
分析：由BE=DF，∠EBC=∠CDF=90°，BC=CD可得△EBC≌△FDC，从而CE=CF．
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCB=45°，请你利用（1）的思路证明：GE=BE+GD．
（3）运用（1）、（2）解答中所积累的经验和知识，完成下题：
如图3，在四边形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求四边形ABCD的面积．

12．阅读材料，解答问题：
为了解方程（x²-1）²-5（x²-1）+4=0，如果我们把x²-1看作一个整体，然后设x²-1=y…①，则原方程可化为y²-5y+4=0，易得y₁=1，y₂=4．
当y=1时，即：x²-1=1，∴x=±$\sqrt{2}$；
当y=4时，即：x²-1=4，∴x=±$\sqrt{5}$，
综上所求，原方程的解为：x₁=$\sqrt{2}$，x₂=-$\sqrt{2}$，x₃=$\sqrt{5}$，x₄=-$\sqrt{5}$．我们把以上这种解决问题的方法通常叫换元法，这种方法它体现了数学中复杂问题简单化、把未知化成已知的转化思想；请根据这种思想完成：
（1）直接应用：解方程x⁴-x²-6=0．　
（2）间接应用：已知实数m，n满足：m²-7m+2=0，n²-7n+2=0，则$\frac{n}{m}$+$\frac{m}{n}$的值是D．
A.$\frac{15}{2}$   B.$\frac{45}{2}$   C.$\frac{15}{2}$或2   D.$\frac{45}{2}$或2
（3）拓展应用：已知实数x，y满足：$\frac{4}{{x}^{4}}$-$\frac{2}{{x}^{2}}$=3，y⁴+y²=3，求$\frac{4}{{x}^{4}}$+y⁴的值．

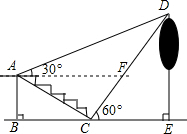11．某校数学兴趣小组的同学为了利用所学知识，测量校园内一棵树DE的高度（如图所示），当这棵树顶点D的影子刚好落在旗台的台阶下点C处时，他们测得此时树顶点D的仰角为60°；当点D的影子刚好落在台阶上点A时，树顶点D的仰角为30°，台阶坡度为$\sqrt{3}$：3，台阶高度AB=2米，点B、C、E在同一水平线上，求树高DE（测角仪高度忽略不计）．