
科目: 来源: 题型:解答题
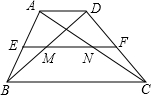 如图,在四边形ABCD中,AD∥BC,AD<BC,中位线EF分别交AC、BD于N、M.
如图,在四边形ABCD中,AD∥BC,AD<BC,中位线EF分别交AC、BD于N、M.查看答案和解析>>
科目: 来源: 题型:解答题
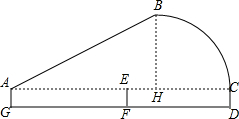 小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)
小明代表学校在邵阳市羽毛球比赛中,击出如图所示的球,其中A-B-C-D代表球飞行的弧度,经测量,小明同学击球时站在距离球网5m的G处,球网在点F处,而球落在球网对面的D处,DF=5m,击出球的角度约为30°,小明的击球高度约为1.6米,近似地把BC段看成$\frac{1}{4}$的圆,∠BHC=90°.比赛完后,小明想知道该球飞行的路程(即线段AB-C-D长)与球最高点B的高度,请你运用所学的知识帮他计算以下.($\sqrt{3}$≈1.73,π≈3.14,结果精确到0.1m)查看答案和解析>>
科目: 来源: 题型:解答题
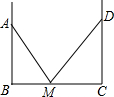 如图,装修师傅装修一间房子,在两墙之间有一个底端在点M的梯子,当它靠在一侧墙上时,梯子的顶端在点A,当它靠在另一侧墙上时,梯子的顶端在点D,已知∠AMB=55°,∠DMC=44°,点A到地面的垂直距离为4m,求点D到地面垂直的距离.(参考数据:sin55°≈0.8192,sin44°≈0.6947)
如图,装修师傅装修一间房子,在两墙之间有一个底端在点M的梯子,当它靠在一侧墙上时,梯子的顶端在点A,当它靠在另一侧墙上时,梯子的顶端在点D,已知∠AMB=55°,∠DMC=44°,点A到地面的垂直距离为4m,求点D到地面垂直的距离.(参考数据:sin55°≈0.8192,sin44°≈0.6947)查看答案和解析>>
科目: 来源: 题型:选择题
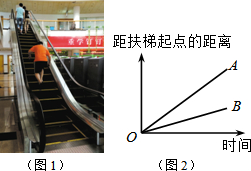 大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )
大明因急事在运行中的自动扶梯上行走去二楼(如图1),图2中线段OA、OB分别表示大明在运行中的自动扶梯上行走去二楼和静止站在运行中的自动扶梯上去二楼时,距自动扶梯起点的距离与时间之间的关系.下面四个图中,虚线OC能大致表示大明在停止运行(即静止)的自动扶梯上行走去二楼时,距自动扶梯起点的距离与时间关系的是( )| A. | 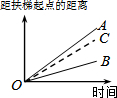 | B. | 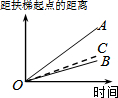 | C. | 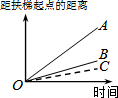 | D. | 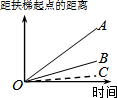 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
| 商品 | 成本价(元/个) | 销售价(元/个) |
| 甲 | 20 | 40 |
| 乙 | 30 | 60 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
| 服装价格 | 甲 | 乙 |
| 进价(元/件) | m | m-20 |
| 售价(元/件) | 240 | 160 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com