
科目: 来源: 题型:解答题
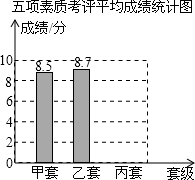 我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)
我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 甲 | 10 | 10 | 7 | 10 | 6 |
| 乙 | 10 | 8 | 8 | 9 | 8 |
| 丙 | 9 | 10 | 9 | 6 | 9 |
| 班级 | 平均数 | 众数 | 中位数 |
| 甲 | 8.6 | 10 | 10 |
| 乙 | 8.6 | 8 | 8 |
| 丙 | 8.6 | 9 | 9 |
查看答案和解析>>
科目: 来源: 题型:解答题
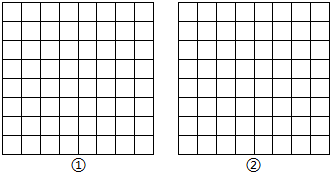 如图,正方形网格中的每一个小正方形的边长都是1,每个小正方形的顶点叫格点,以格点为顶点分别在图①、图②中,画三角形和平行四边形.
如图,正方形网格中的每一个小正方形的边长都是1,每个小正方形的顶点叫格点,以格点为顶点分别在图①、图②中,画三角形和平行四边形.查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目: 来源: 题型:解答题
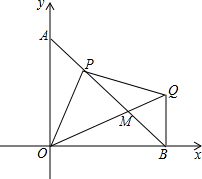 已知:如图,A、B两点坐标为(0,4),B(4,0),P为线段AB上的任一点,过P作OP的垂线与过B点的x轴的垂线交于点Q,OQ与直线AB交于点M.请探究解答下列问题:
已知:如图,A、B两点坐标为(0,4),B(4,0),P为线段AB上的任一点,过P作OP的垂线与过B点的x轴的垂线交于点Q,OQ与直线AB交于点M.请探究解答下列问题:查看答案和解析>>
科目: 来源: 题型:填空题
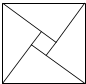 四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为1,大正方形面积为13,直角三角形的两条直角边为a、b,那么(a+b)2的值是25.
四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形,这样就组成了一个“赵爽弦图”(如图).如果小正方形面积为1,大正方形面积为13,直角三角形的两条直角边为a、b,那么(a+b)2的值是25.查看答案和解析>>
科目: 来源: 题型:选择题
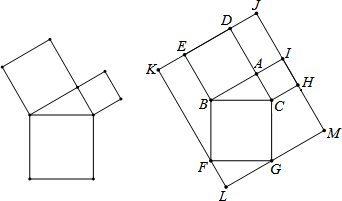
| A. | 48+20$\sqrt{3}$ | B. | 32+20$\sqrt{3}$ | C. | 52+16$\sqrt{3}$ | D. | 28+16$\sqrt{3}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
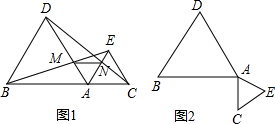
查看答案和解析>>
科目: 来源: 题型:填空题
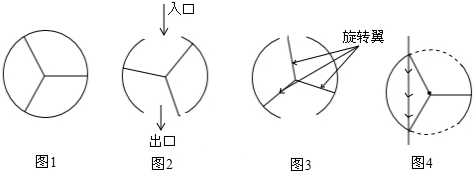
查看答案和解析>>
科目: 来源: 题型:解答题
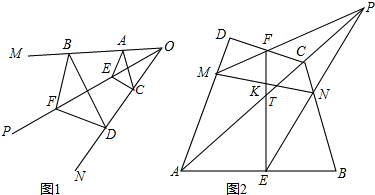
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com