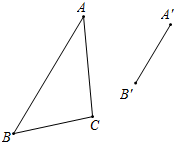3．如图，已知△ABC和△A′B′C′是位似比为2的位似三角形，且AB的对应边是A′B′，请用尺规作图，将△A′B′C′补充完整（可不写作法，但保留作图痕迹）．

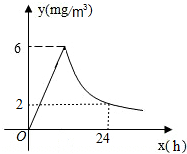2．每年春季为预防流感，某校利用休息日对教室进行药熏消毒，已知药物燃烧过程及燃烧完后空气中的含药量y（mg/m³）与时间x（h）之间的关系如图所示，根据消毒要求，空气中的含药量不低于3mg/m³且持续时间不能低于10h．请你帮助计算一下，当空气中的含药量不低于3mg/m³时，持续时间可以达到12h．

1．下面的三个图形是由若干个小正方形搭建而成的几何体的三视图，组成几何体的小正方形个数是（　　）

A．

7

B．

6

C．

5

D．

4

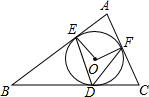20．如图，⊙O内切于△ABC，切点分别为D，E，F，连接OE，OF，DE，DF，乙组∠A=80°，则∠EDF等于（　　）

A．

40°

B．

45°

C．

50°

D．

80°

19．甲、乙两个兴趣小组参加了某次知识竞赛，辅导老师对两个小组竞赛成绩进行了统计，得到以下数据：$\overline{{x}_{甲}}$=79，$\overline{{x}_{乙}}$=82，S_甲²=82，S_乙²=79，则这两个小组成员的成绩比较稳定的是（　　）

A．

甲组

B．

乙组

C．

两组一样

D．

无法确定

18．学生的学业负担过重会严重影响学生对待学习的态度．为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查（把学习态度分为三个层级，A级：对学习很感兴趣；B级：对学习较感兴趣；C级：对学习不感兴趣），并将调查结果绘制成图①和图②的统计图（不完整）．请根据图中提供的信息，解答下列问题：
（1）此次抽样调查中，共调查了200名学生；
（2）将图①补充完整；
（3）求出图②中C级所占的圆心角的度数；
（4）根据抽样调查结果，请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标（达标包括A级和B级）？

17．教材在探索平方差公式时利用了面积法，面积法除了可以帮助我们记忆公式，还可以直观地推导或验证公式，俗称“无字证明”，例如，著名的赵爽弦图（如图①，其中四个直角三角形较大的直角边长都为a，较小的直角边长都为b，斜边长都为c），大正方形的面积可以表示为c²，也可以表示为4×$\frac{1}{2}ab+{（a-b）^2}$由此推导出重要的勾股定理：如果直角三角形两条直角边长为a，b，斜边长为c，则a²+b²=c²．
（1）图②为美国第二十任总统伽菲尔德的“总统证法”，请你利用图②推导勾股定理．
（2）如图③，直角△ABC中，∠ACB=90°，AC=3cm，BC=4cm，则斜边AB上的高CD的长为$\frac{12}{5}$cm．
（3）试构造一个图形，使它的面积能够解释（a+b）（a+2b）=a²+3ab+2b²，画在如图4的网格中，并标出字母a、b所表示的线段．

16．如图，直线l₁∥l₂，l₃⊥l₄，∠1=44°，那么∠2的度数（　　）

A．

46°

B．

44°

C．

36°

D．

22°

15．如图，在?ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中成立的有①②③．（只填序号）
①∠DCF=$\frac{1}{2}$∠BCD；②EF=CF；③∠DFE=3∠AEF．

14．[问题情境]
勾股定理是一条古老的数学定理，它有很多种证明方法．我国汉代数学家赵爽根据弦图，利用面积法进行证明，著名数学家华罗庚曾提出把“数学关系”（勾股定理）带到其它星球，作为地球人与其他星球“人”进行第一次“谈话”的语言；
[定理表述]请你根据图1中的直角三角形叙述勾股定理；
[尝试证明]以图1中的直角三角形为基础，将两个直角边长为a，b，斜边长为c的三角形按如图所示的方式放置，连接两个之间三角形的另外一对锐角的顶点（如图2），请你利用图2，验证勾股定理；
[知识扩展]利用图2中的直角梯形，我们可以证明$\frac{a+b}{c}$＜$\sqrt{2}$，其证明步骤如下：
∵BC=a+b，AD=$\sqrt{2}c$
又∵在直角梯形ABCD中，有BCAD（填大小关系），即BC＜AD
∴$\frac{a+b}{c}$$＜\sqrt{2}$．