6．某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．求销售单价为多少元时，每天的销售利润最大？最大利润是多少？

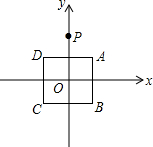5．正方形ABCD在坐标系中位置如图所示，作点P（0，2）关于点A的对称点P₁，点P₁关于点B的对称点P₂，点P₂关于点C的对称点P₃，点P₃关于点D的对称点P₄，…，按此操作下去，则点P₂₀₁₄的坐标为（　　）

A．

（0，2）

B．

（2，0）

C．

（0，-2）

D．

（-2，0）

4．观察下列化简过程：
①$\sqrt{\frac{2}{3}}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{2}×\sqrt{3}}{\sqrt{3}×\sqrt{3}}$=$\frac{\sqrt{6}}{3}$
②$\frac{1}{\sqrt{18}}$=$\frac{1}{3\sqrt{2}}$=$\frac{1×\sqrt{2}}{3\sqrt{2}×\sqrt{2}}$=$\frac{\sqrt{2}}{6}$
③$\frac{1}{\sqrt{2}+1}$=$\frac{1×（\sqrt{2}-1）}{（\sqrt{2}+1）（\sqrt{2}-1）}$=$\sqrt{2}$-1
以上过程都是通过恒等值变形，将分母的根号（或根号中的分母）去掉，我们把这个过程叫做分母有理化，变形中分子分母分别乘的式子叫做它们的有理化因式，如①中的有理化因式是$\sqrt{3}$，②中的有理化因式是$\sqrt{2}$，③中的有理化因式是$\sqrt{2}$-1，解答下列问题：
（1）二次根式$\frac{1}{\sqrt{27}}$、$\sqrt{\frac{3}{8}}$、$\frac{3}{\sqrt{7}-2}$的有理化因式分别为$\sqrt{3}、\sqrt{2}、\sqrt{7}+2$；
（2）第（1）题中二次根式化简的结果分别为$\frac{\sqrt{3}}{9}、\frac{\sqrt{6}}{4}、\sqrt{7}+2$；
（3）计算：（$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{2+\sqrt{3}}$+…+$\frac{1}{\sqrt{99}+\sqrt{98}}$）×（$\sqrt{99}$+1）

3．先化简，再求值：（b-2a）（-2a+b）+b（2a+b）-4a²b÷b，其中a=-$\frac{1}{2}$，b=2．

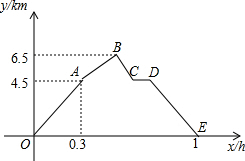2．从甲地到乙地，先是一段平路，然后是一段上坡路，小明骑车从甲地出发，到达乙地后立即原路返回甲地，途中休息了一段时间，假设小明骑车在平路、上坡、下坡时分别保持匀速前进．已知小明骑车上坡的速度比在平路上的速度每小时少5km，下坡的速度比在平路上的速度每小时多5km．设小明出发x h后，到达离甲地y km的地方，图中的折线OABCDE表示y与x之间的函数关系．如果小明两次经过途中某一地点的时间间隔为0.12h，那么该地点离甲地5.7km．

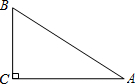1．如图，在Rt△ABC中，∠C=90°，∠A=30°，BC=1，
（1）则AC的长为$\sqrt{3}$；
（2）若点D在AC上，将△ADB沿直线BD翻折后，使点A落在点E处，如果AD⊥ED，那么线段DE的长为$\sqrt{3}$-1．

20．如图1，已知正方形ABCD，点E是边AB的中点，点O是线段AE上的一个动点（不与A、E重合），以O为圆心，OB为半径的圆与边AD相交于点M，过点M作⊙O的切线交DC于点N．
（1）求证：MN=AM+CN；
（2）如图2，延长MA交⊙O于点F，连接EN，若AF=4，AO：BO=3：5，求EN的长．

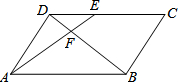19．如图，在平行四边形ABCD中，E为CD上一点，连接AE、BD，且AE、BD交于点F，S_△DEF：S_△ABF=4：25，则S_△ADF：S_{四边形BCEF}为（　　）

A．

10：31

B．

10：21

C．

4：25

D．

4：21

18．如图是立方体和长方体模型，棱长如图所示，现用60张长为6，宽为4的长方形卡纸，剪出这两种模型的表面展开图，如图2，每张卡纸剪出3个立方体的表面展开图（图中只画出1个）；
如图3，每张卡纸剪出2个长方体的展开图；
（1）在图2中画出另外两个立方体的表面展开图，用不同的阴影表示；
（2）设用x张卡纸做立方体，其余做长方体，共做两种模型y个，写出y关于x的函数关系式；
（3）设每个模型（包括立方体和长方体）平均获利为w（元），w满足函数w=1.6-$\frac{x}{100}$，这些模型作为教具卖出共获利196元，问立方体和长方体各做了多少个？

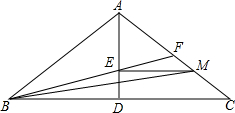17．如图，在等腰三角形ABC中，AD⊥BC于点D，AD=3，DC=4，点M在线段AC上运动，ME⊥AD于点E，连结BE并延长交AC于点F，连结BM．设$\frac{CM}{AC}$=m（0＜m＜1），△BEM的面积为S．
（1）当m=$\frac{1}{3}$时，求$\frac{{{S_{△ABE}}}}{{{S_{△BME}}}}$的值．
（2）求S关于m（0＜m＜1）的函数解析式并求出S的最大值．
（3）设$\frac{AF}{FM}$=k，猜想k与m的数量关系并证明．