科目： 来源： 题型：选择题

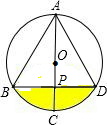3．如图，已知在⊙O中，AB=4$\sqrt{3}$，AF=6，AC是直径，AC⊥BD于F，图中阴影部分的面积是（　　）

A．

$\frac{8}{3}$π-2$\sqrt{3}$

B．

$\frac{16}{3}$π-2$\sqrt{3}$

C．

$\frac{8}{3}$π-4$\sqrt{3}$

D．

$\frac{16}{3}$π-4$\sqrt{3}$

科目： 来源： 题型：选择题

科目： 来源： 题型：选择题

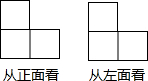1．如图，是由若干个完全相同的小正方体组成的一个几何体的从正面看和从左面看的图形，则组成这个几何体的小正方体的个数是（　　）

A．

3个或4个或5个

B．

4个或5个

C．

5个或6个

D．

6个或7个

科目： 来源： 题型：选择题

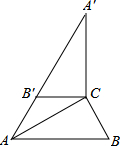20．如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2．将△ABC绕点C顺时针旋转得到△A′B′C，连结AB′．若A、B′、A′在同一条直线上，则AA′的长为（　　）

A．

6

B．

$4\sqrt{3}$

C．

$3\sqrt{3}$

D．

3

科目： 来源： 题型：解答题

19．某中学综合实践小组同学，想测量金龙山观音大佛的高度，他们在山脚下的D处测得山顶B的仰角为30°，沿着山脚向前走了4米达到E处，测得观音大佛的头顶A的倾角为45°，已知金龙山的山顶距地面的标高（线段BC的长度）为60米，请计算观音大佛的高度为多少米？（结果精确到0.1米，$\sqrt{3}$≈1.73）

科目： 来源： 题型：填空题

18．小慧把边长为1的正方形纸片0ABC放在直线l₂上，0A边与直线l₂重合，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时点O运动到了点O₁处（即点B处），点C运动到了点C₁处，点B运动到了点B₂处，小慧又将正方形纸片 AO₁C₁B₁绕顶点B₁按顺时针方向旋转90°，…．正方形纸片OABC按上述方法经过81次旋转，顶点0经过的路程是$\frac{{41+20\sqrt{2}}}{2}π$．

科目： 来源： 题型：选择题

科目： 来源： 题型：填空题

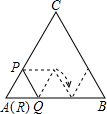16．如图，正△ABC的边长为9cm，边长为3cm的正△RPQ的顶点R与点A重合，点P，Q分别在AC，AB上，将△RPQ沿着边AB，BC，CA连续翻转（如图所示），直至点P第一次回到原来的位置，则点P运动路径的长为6πcm．（结果保留π）

科目： 来源： 题型：解答题

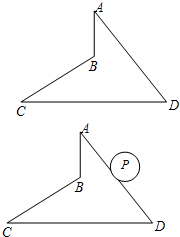15．如图，四边形ABCD中，已知∠A=∠C=30°，∠D=60°，AD=8，CD=10．
（1）求AB、BC的长；
（2）已知，半径为1的⊙P在四边形ABCD的外面沿各边滚动（无滑动）一周，求⊙P在整个滚动过程中所覆盖部分图形的面积．

科目： 来源： 题型：填空题

14．如图1，点P是以r为半径的圆O外一点，点P′在线段OP上，若满足OP•OP′=r²，则称点P′是点P关于圆O的反演点．如图2，在Rt△ABO中，∠B=90°，AB=2，BO=4，圆O的半径为2，如果点A′、B′分别是点A、B关于圆O的反演点，那么A′B′的长是$\frac{\sqrt{5}}{5}$．