
科目: 来源: 题型:选择题
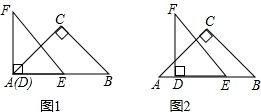 如图1,△ABC和△DEF都是等腰直角三角形,其中∠C=∠EDF=90°,点A与点D重合,点E在AB上,AB=4,DE=2.如图2,△ABC保持不动,△DEF沿着线段AB从点A向点B移动,当点D与点B重合时停止移动.设AD=x,△DEF与△ABC重叠部分的面积为y,则y关于x的函数图象大致是( )
如图1,△ABC和△DEF都是等腰直角三角形,其中∠C=∠EDF=90°,点A与点D重合,点E在AB上,AB=4,DE=2.如图2,△ABC保持不动,△DEF沿着线段AB从点A向点B移动,当点D与点B重合时停止移动.设AD=x,△DEF与△ABC重叠部分的面积为y,则y关于x的函数图象大致是( )| A. |  | B. | 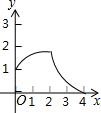 | C. | 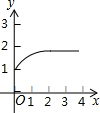 | D. | 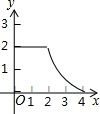 |
查看答案和解析>>
科目: 来源: 题型:选择题
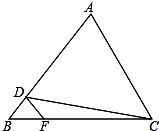 如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )
如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )| A. | 1:16 | B. | 1:18 | C. | 1:20 | D. | 1:24 |
查看答案和解析>>
科目: 来源: 题型:解答题
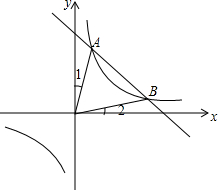 如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).
如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
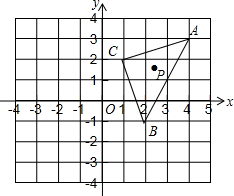 在平面直角坐标系中,△ABC的三个顶点的位置如图,P为△ABC内一点,P的坐标为(a,b).
在平面直角坐标系中,△ABC的三个顶点的位置如图,P为△ABC内一点,P的坐标为(a,b).查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
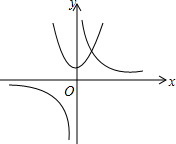 请阅读下列内容:我们在平面直角坐标系中画出抛物线y=x2+1和双曲线y=$\frac{2}{x}$,如图所示,利用两图象的交点个数和位置来确定方程x2+1=$\frac{2}{x}$有一个正实数根,这种方法称为利用的图象判断方程根的情况请用图象法判断方程-(x-3)2+4=$\frac{2}{x}$的根的情况两个正根一个负根(填写根的个数及正负).
请阅读下列内容:我们在平面直角坐标系中画出抛物线y=x2+1和双曲线y=$\frac{2}{x}$,如图所示,利用两图象的交点个数和位置来确定方程x2+1=$\frac{2}{x}$有一个正实数根,这种方法称为利用的图象判断方程根的情况请用图象法判断方程-(x-3)2+4=$\frac{2}{x}$的根的情况两个正根一个负根(填写根的个数及正负).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com