
科目: 来源: 题型:解答题
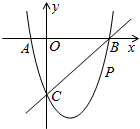 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点左侧,B点的坐标为(4,0),与y轴交于C(0,-4)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点左侧,B点的坐标为(4,0),与y轴交于C(0,-4)点,点P是直线BC下方的抛物线上一动点.查看答案和解析>>
科目: 来源: 题型:解答题
 如图,二次函数y=-$\frac{\sqrt{3}}{3}{x}^{2}-\frac{2}{3}\sqrt{3}x+\sqrt{3}$的图象交x轴于A,B两点,交y轴于点C,顶点为D.
如图,二次函数y=-$\frac{\sqrt{3}}{3}{x}^{2}-\frac{2}{3}\sqrt{3}x+\sqrt{3}$的图象交x轴于A,B两点,交y轴于点C,顶点为D.查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:解答题
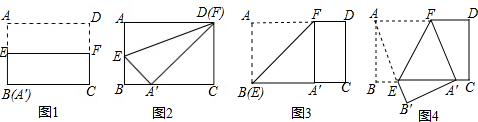
查看答案和解析>>
科目: 来源: 题型:解答题
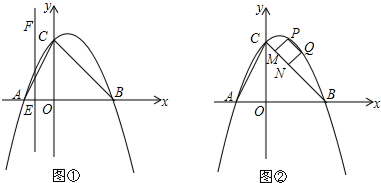
查看答案和解析>>
科目: 来源: 题型:解答题
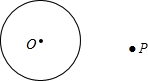 我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)
我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目: 来源: 题型:填空题
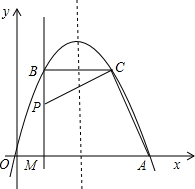 如图,经过原点的抛物线y=-x2+mx(m>2)与x轴的另一交点为A,过点P(1,$\frac{m}{2}$)作直线PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连接CB,CP,CA,要使得CA⊥CP,则m的值为3.
如图,经过原点的抛物线y=-x2+mx(m>2)与x轴的另一交点为A,过点P(1,$\frac{m}{2}$)作直线PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连接CB,CP,CA,要使得CA⊥CP,则m的值为3.查看答案和解析>>
科目: 来源: 题型:解答题
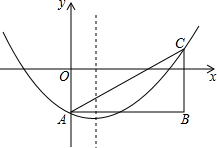 如图,在平面直角坐标系中,抛物线y=ax2-2ax-2(a>0)与y轴交于点A,点B的坐标为($\frac{1}{a}$,-2),过点B作y轴的平行线,交抛物线于点C,连结AB、AC.
如图,在平面直角坐标系中,抛物线y=ax2-2ax-2(a>0)与y轴交于点A,点B的坐标为($\frac{1}{a}$,-2),过点B作y轴的平行线,交抛物线于点C,连结AB、AC.查看答案和解析>>
科目: 来源: 题型:选择题
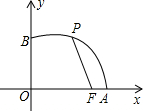 如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( )
如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( )| A. | ①②③ | B. | ①③ | C. | ①②④ | D. | ③④ |
查看答案和解析>>
科目: 来源: 题型:解答题
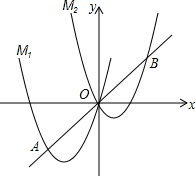 如图,将抛物线M1:y=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线y=x与M1的一个交点记为A,与M2的一个交点记为B,点A的横坐标是-3.
如图,将抛物线M1:y=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线y=x与M1的一个交点记为A,与M2的一个交点记为B,点A的横坐标是-3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com