
科目: 来源: 题型:解答题
 观察探究,完成证明和填空.如图,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H得到的四边形EFGH叫做中点四边形.
观察探究,完成证明和填空.如图,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H得到的四边形EFGH叫做中点四边形.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
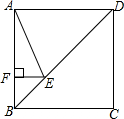 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )| A. | 4-2$\sqrt{2}$ | B. | 3$\sqrt{2}$-4 | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | $\sqrt{{a}^{2}}$=a | B. | $\sqrt{{a}^{2}}$=a2 | C. | $\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$ | D. | $\sqrt{ab}$=$\sqrt{a}$$•\sqrt{b}$ |
查看答案和解析>>
科目: 来源: 题型:解答题
 在平面直角坐标系中,若横坐标、纵坐标均为整数点称为格点,若一个多边形的顶点都是格点,则称为格点多边形.记格点多边形的面积为S,其内部的格点数记为n,边界上的格点数记为l,例如图中△ABC是格点三角形,对应的S=1,n=0,l=4.
在平面直角坐标系中,若横坐标、纵坐标均为整数点称为格点,若一个多边形的顶点都是格点,则称为格点多边形.记格点多边形的面积为S,其内部的格点数记为n,边界上的格点数记为l,例如图中△ABC是格点三角形,对应的S=1,n=0,l=4.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com