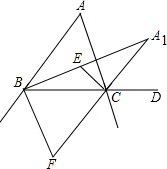16．如图，在△ABC中，点E是∠ABC、∠ACB角平分线的交点，点F是∠ABC、∠ACB外角平分线的交点，点A₁是内角∠ABC、外角∠ACD平分线的交点．
（1）若∠A=70°，则∠A₁EC=55°°；∠BFC=55°°；
（2）探究：∠BEC与∠BFC满足何种数量关系？并简要说明理由；
（3）若∠A=m°，在前面的情况下，继续作∠A₁BC与∠A₁CD的平分线交于点A₂，∠A₂BC与∠A₂CD的平分线交于点A₃，…，以此类推，∠A₂₀₁₂BC与∠A₂₀₁₂CD的平分线交于点A₂₀₁₃，探求∠A₂₀₁₃的度数 （用m的关系式表示，直接写出结果）．

15．如图，抛物线C₁：y=ax²+2ax+4与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，M为此抛物线的顶点，若△ABC的面积为12．
（1）求此抛物线的函数解析式；
（2）动直线l从与直线AC重合的位置出发，绕点A顺时针旋转，与直线AB重合时终止运动，直线l与BC交于点D，P是线段AD的中点．
①直接写出点P所经过的路线长为$\sqrt{5}$；
②点D与B、C不重合时，过点D作DE⊥AC于点E，作DF⊥AB于点F，连接PE、PF、EF，在旋转过程中，求EF的最小值；
（3）将抛物线C₁平移得到抛物线C₂，已知抛物线C₂的顶点为N，与直线AC交于E、F两点，若EF=AC，求直线MN的解析式．

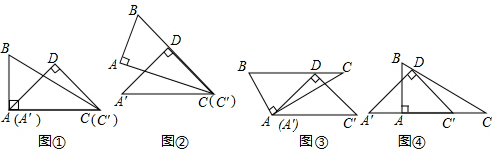
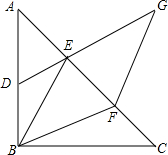14．已知∠ABC=90°，AB=BC，F为AC上一点，D，E分别为AB，AF的中点，连接BF，过F作FG∥BE交DE的延长线于G，连接BE，且BE=2DE，AC=6$\sqrt{2}$
（1）求证：四边形BEGF为菱形；
（2）求四边形BEGF的面积；
（3）连接AG，GC，则四边形ABCG为何种特殊的四边形，请说明理由；
（4）M为四边形ABCG边上一点，AM交DG于N点，且满足AM=BG，求AN的长度．

13．如图，正方形ABCD中，点P是直线BC上一点，连接PA，将线段PA绕点P逆时针旋转90°得到线段PE，在直线BA上取点F，使BF=BP，且点F与点E在BC同侧，连接EF、CF．
（1）如图①，当点P在CB延长线上时，求证：四边形PCFE是平行四边形．
（2）如图②，当点P在线段BC上时，四边形PCFE是否还是平行四边形，说明理由．

12．现有一副直角三角板，已知含45°角的直角三角板的斜边恰与含30°角的直角三角板的较长直角边完全重合（如图①）．即△C′DA′的顶点A′、C′分别与△BAC的顶点A、C重合．现在让△C′DA′固定不动，将△BAC通过变换使斜边BC经过△C′DA′的直角顶点D．
（1）如图②，将△BAC绕点C按顺时针方向旋转角度α（0°＜α＜180°），使BC边经过点D，则α=15°
（2）如图③，将△BAC绕点A按逆时针方向旋转，使BC边经过点D．试说明：BC∥A′C′．
（3）如图④，若将△BAC沿射线A′C′方向平移m个单位长度，使BC边经过点D，已知AB=2$\sqrt{3}$，求m的值．

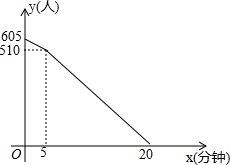11．“五．一”假期，某火车客运站旅客流量明显增大，动车一般在开车前30分钟开始检票．假设某趟动车开始检票时已有605人到候车室排队检票，在检票开始5分钟内每分钟还有5个旅客进候车室进行检票，5分钟后到检票结束每分钟还会有2人到候车室排队检票，每分钟每个检票窗口检票12人（火车站会根据候车人数调研开放检票窗口数）．此趟动车候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．根据关系图解答下列问题：
（1）在检票开始5分钟内，火车站有2个检票窗口开放检票；
（2）设开始检票5-20分钟期间，候车室排队等候检票的旅客人数y与时间t的关系为一次函数y=kx+b（5≤t≤20），求这个函数解析式；
（3）若候车按原计划开放检票口数，并且开始检票5分钟内每分钟检票人数不变，但要在开始检票18分钟时让排队的旅客都能检票入站，以便后来到站随到随检，求5分钟每个检票口每分钟至少要多检的旅客数（假定此处多检的旅客数可以为分数）．

10．已知：如图所示，在△ABO中，∠AOB=90°，AO=6cm，BO=8cm，AB=10cm．且两直角边落在平面直角坐标系的坐标轴上．
（1）如果点P从A点开始向O以1cm/s的速度移动，点Q从点O开始向B以2cm/s的速度移动．P，Q分别从A，O同时出发，那么几秒后，△POQ为等腰三角形？
（2）若M，N分别从A，O出发在三角形的边上运动，若M点运动的速度是xcm/s，N点运动的速度是ycm/s，当M，N相向运动时，2s后相遇，当M，N都沿着边逆时针运动时9s后相遇．求M、N的速度．

9．如图1，在梯形ABCD中，BC∥AD，CD⊥AD，动点P从点A出发，以2cm∕s的速度沿AB-BC-CD折线运动，当点P到达点D时停止运动．已知△PAD的面积y（cm²）与点P的运动时间x（s）的函数关系如图2，则a的值为（　　）

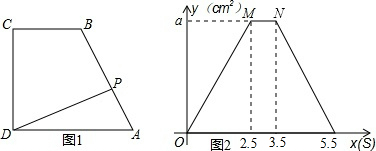
A．

10

B．

14

C．

16

D．

20

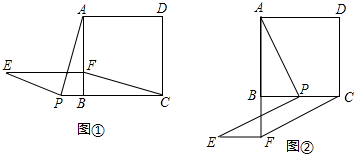
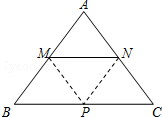8．在等腰△ABC中，AB=AC=5，BC=6．动点M、N分别在两腰AB、AC上（M不与A、B重合，N不与A、C重合），且MN∥BC．将△AMN沿MN所在的直线折叠，使点A的对应点为P．
（1）当MN为何值时，点P恰好落在BC上？
（2）当MN=x，△MNP与等腰△ABC重叠部分的面积为y，试写出y与x的函数关系式．当x为何值时，y的值最大，最大值是多少？
（3）是否存在x，使y等于S_△ABC的四分之一？如果存在，请直接写出x的值；如果不存在，请说明理由．

7．已知：A（1，-2）、B（-1，0）、C（2，0）．建立平面直角坐标系，画出△ABC，并求△ABC的面积．