
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
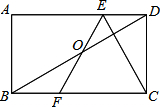 如图,矩形ABCD中,E、F分别是AD、BC上的点,且DE=BF,EF与BD交于点O.
如图,矩形ABCD中,E、F分别是AD、BC上的点,且DE=BF,EF与BD交于点O.查看答案和解析>>
科目: 来源: 题型:填空题
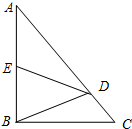 如图,在Rt△ABC中,∠ABC=90°,点D在边AC上,线段DB绕点D顺时针旋转,端点B恰巧落在边AB上的点E处.如果$\frac{AE}{EB}$=y,$\frac{AD}{DC}$=x.那么y与x满足的关系式是:y=$\frac{x-1}{2}$(用含x的代数式表示y).
如图,在Rt△ABC中,∠ABC=90°,点D在边AC上,线段DB绕点D顺时针旋转,端点B恰巧落在边AB上的点E处.如果$\frac{AE}{EB}$=y,$\frac{AD}{DC}$=x.那么y与x满足的关系式是:y=$\frac{x-1}{2}$(用含x的代数式表示y).查看答案和解析>>
科目: 来源: 题型:填空题
 如图,将直线$y=\frac{{\sqrt{3}}}{3}x$向上平移2个单位交坐标轴于点A、D,然后绕AD中点B逆时针旋转60°,三条直线与y轴围成四边形ABCO,若四边形始终覆盖着二次函数y=x2-2mx+m2-1图象的一部分,则满足条件的实数m的取值范围为-$\sqrt{3}$-$\sqrt{2}$≤m≤$\sqrt{3}$.
如图,将直线$y=\frac{{\sqrt{3}}}{3}x$向上平移2个单位交坐标轴于点A、D,然后绕AD中点B逆时针旋转60°,三条直线与y轴围成四边形ABCO,若四边形始终覆盖着二次函数y=x2-2mx+m2-1图象的一部分,则满足条件的实数m的取值范围为-$\sqrt{3}$-$\sqrt{2}$≤m≤$\sqrt{3}$.查看答案和解析>>
科目: 来源: 题型:解答题
 (1)实数a、b在数轴上的位置如图所示,请化简:|a|-$\sqrt{a^2}-\sqrt{b^2}$;
(1)实数a、b在数轴上的位置如图所示,请化简:|a|-$\sqrt{a^2}-\sqrt{b^2}$;查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
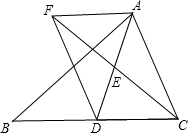 已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.查看答案和解析>>
科目: 来源: 题型:解答题
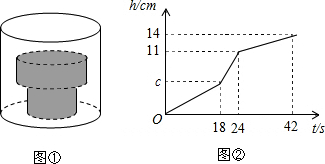
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com