18．在△ABC中，BA=BC，∠BAC=α，M是AC的中点，P是线段BM上的动点，将线段PA绕点P顺时针旋转2α转得到线段PQ．
（1）若α=60°且点P与点M重合（如图1），线段CQ的延长线交射线BM于点D．求∠CDB的度数；
（2）在图2中，点P不与点B，M重合，线段CQ的延长线于射线BM交于点D，求∠CDB的大小（用含α的代数式表示）；
（3）对于适当大小的α，当点P在线段BM上运动到某一位置（不与点B，M重合）时，能使得线段CQ的延长线与射线BM交于点D，且PQ=QD，请求α的取值范围．

17．近年来，国家大力提倡大学生创业，2015年小王就要毕业了，因为他学的是市场营销专业，所以毕业后想开一个商店，经过市场调研发现，若投资一个面积为x（单位：m²）的商铺，所需购买费用（单位：万元）与x+2成正比例，装修费用（单位：万元）与x²成正比例，并在调查过程中得到了表格中的数据：

商铺的面积（m2）	购买费用（万元）	装修费用（万元）
1	1.8	0.3

（1）如果小王用从银行贷款30万元、父亲资助20万元、自己大学期间勤工俭学的收入1.6万元，共51.6万元投资一个商铺，请计算小王投资的这个商铺的面积为多少平方米；（总费用=购买费用+装修费用）
（2）购买商铺后，小王准备经营童鞋专卖店，已知专卖店代理的某品牌童鞋的进价为每双40元，该品牌童鞋日销售量y（双）与销售单价x（元/双）之间的关系式为：
y=$\left\{\begin{array}{l}{-2x+140（40≤x≤58）}\\{-x+82（58＜x≤71）}\end{array}\right.$
①求他的销售利润w（元）与销售单价x（元/双）之间的函数关系式．
②小王每月需向银行还贷2075元，另童鞋店每月需缴纳水电费、营业税等固定费用3000元，通过计算判断，小王每月（按30天计算）能否有盈余？如果有，最多盈余多少元？（盈余=销售利润-固定费用-银行贷款）

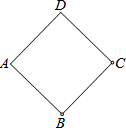16．如图，正方形ABCD，边长AB=2．
（1）画出正方形ABCD绕A点顺时针旋转45°后的正方形AB′C′D′；
（2）若CB与C′D′相交于点E，求四边形ABED′的面积．

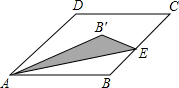15．如图，已知在周长为20的菱形ABCD中，∠C=45°，点E是线段BC上一点，将△ABE沿AE所在直线翻折，使点B落在B′上，则在点E沿B→C→D运动的过程中，点B′运动的路径长是$\frac{5π}{4}$．

14．如图，把一张对边平行的长方形ABCD（AD∥BC，AB∥DC）的纸片沿EF折叠后，ED、BC的交点为G，点D、C分别落在D′C′的位置上，若∠EFG=55°，求∠EGF的度数．

13．如图，已知长方形纸片ABCD，AB=CD，AD=BC，现将长方形纸片ABCD沿对角线AC对折，使点B落在点E处，试说明DF=EF．

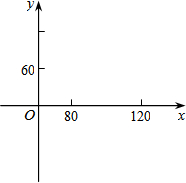12．一种产品的进价为40元，某公司在销售这种产品时，每年总开支为100万元（不含进价）．经过若干年销售得知，年销售量y（万件）是销售单价x（元）的一次函数，并得到如下部分数据：

销售单价x（元）	50	60	70	80
年销售量y（万件）	5.5	5	4.5	4

（1）求y关于x的函数关系式；
（2）写出该公司销售这种产品的年利润w（万元）关于销售单价x（元）的函数关系式；当销售单价x为何值时，年利润最大？
（3）试通过（2）中的函数关系式及其大致图象帮助该公司确定产品的销售单价范围，使年利润不低于60万元．

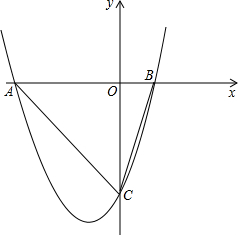11．已知抛物线y=x²+2x-3与x轴交于A，B（点A在点B的左侧）两单，与y轴交于点C．
（1）填空：点B的坐标是（1，0），直线AC的函数关系式为y=-x-3；
（2）设点D（-2，a），请问，当a为何值时，DB+DC值最小？
（3）若直线AC上是否存在一点P，使以点A、O、P为顶点的三角形与△ABC相似？若存在，请求出P点的坐标；若不存在，请说明理由．

10．如图①，是某设计师设计的一建筑物造型的纵截面，曲线OBA是一开口向右、对称轴正好是水平线OC的抛物线的一部分，AC、BD是与水平线OC垂直的两根支柱，AC=5米，BD=3米，OD=3米．

（1）请你利用所学的函数知识求OC的长（在所给的方框内画出函数图象的草图，并在图中标出点O、A、B、C、D对应的位置）；
（2）为了安全美观，准备拆除支柱AC、BD，在水平线OC上另找一点P作为地面上的支撑点，用固定材料连接PA、PB，对抛物线造型进行支撑加固．（如图②）
①为使用料最省，请在图②中作出用料最省时的点Po的位置；（支柱与地面、造型连接处的用料多少问题暂不考虑）
②计算用料最省时点O、P之间的距离是多少？

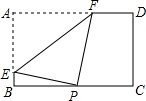9．如图，矩形纸片ABCD中，AB=4，AD=6，点P是边BC上的动点，现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别为E、F，要使折痕始终与边AB、AD有交点，则BP的取值范围是6-2$\sqrt{5}$≤x≤4．