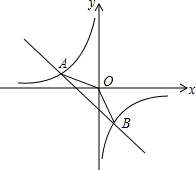18．如图，在平面直角坐标系xOy中，一次函数y₁=ax+b（a，b为常数，且a≠0）与反比例函数y₂=$\frac{m}{x}$（m为常数，且m≠0）的图象交于点A（-2，1）、B（1，n）．
（1）求反比例函数和一次函数的解析式；
（2）连结OA、OB，求△AOB的面积；
（3）直接写出当y₁＜y₂＜0时，自变量x的取值范围．

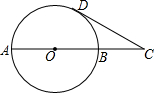17．如图，已知AB是⊙O的一条直径，延长AB至C点，使AC=3BC，CD与⊙O相切于D点．若CD=$\sqrt{3}$，则劣弧AD的长为$\frac{2}{3}$π．

16．如图，正方形ABCD和正△AEF都内接于⊙O，EF与BC、CD分别相交于点G、H，则$\frac{EF}{GH}$的值是（　　）

A．

$\frac{\sqrt{6}}{2}$

B．

$\sqrt{2}$

C．

$\sqrt{3}$

D．

2

15．已知四边形ABCD是正方形
（1）如图1．点M在边BA的延长线上，点N在边BC上，且AM=CN，连接MN，DM，DN，判断△DMN的形状（直接写出答案）．
（2）如图2，当店N在边AB上，点N在边BC的延长线上，AM=CN，连接MN，取线段MN的中点G，连接DG，DM，判断线段DG和线段MG的关系并说明理由．
（3）如图3，当点M在边AB的延长线上，点N在边BC的延长线上，AM=CN，连接MN，DM，DN，点G是线段MN的中点，连接BG，DG，连接GC并延长交BD于点H，若∠AMN=75°，判断线段GH和线段BD的关系并说明理由．

14．如图，在△ABC中，∠C=90°，D为边BC上一点，E为BA延长线上一点，EF⊥AB交CA的延长线于F，EF=CD，连接DE交AC于G
（1）若∠BAC=30°，求$\frac{DG}{EG}$的值；
（2）如图2，若点H为边AB上一点，且HD=HB，求证：AH=DH+AF．

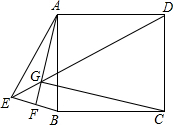13．已知E是正方形ABCD外一点，且AB=AE，连BE作AF⊥BE，垂足为F，连DE交AF于G．
（1）求∠AGD的度数；
（2）连CG，求$\frac{AG+CG}{DG}$的值；
（3）若EG=2，DG=6，则正方形ABCD的边长为2$\sqrt{5}$．

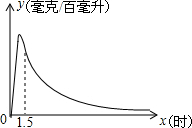12．实验数据显示：一般成人喝半斤低度白酒后，1.5小时内（包括1.5小时）其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可近似地用二次函数y=-200x²+400x表示；1.5小时后（包括1.5小时）y与x可近似地用反比例函数y=$\frac{k}{x}$（k＞0）表示（如图所示）．
（1）喝酒后多长时间血液中的酒精含量达到最大值？最大值为多少？
（2）求k的值．
（3）按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”，不能驾车上路．参照上述数学模型，假设某驾驶员晚上20：00在家喝完半斤低度白酒，第二天早上7：00能否驾车去上班？请说明理由．

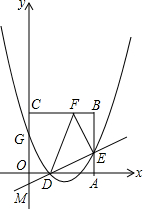11．如图所示，正方形OABC的边长为2cm，以OA、OC所在直线为坐标轴建立直角坐标系xoy，点D、E、F和G分别从点O、A、B和C沿着OA、AB、BC和CO方向都以1cm/s的速度同时移动，移动时间为t（0＜t＜2）s，抛物线y=ax²+bx+c总是经过三个动点G、D、E．
（1）判断△DEF的形状，并说明理由；
（2）△DEF的面积是否存在最大值或最小值？若存在，请求出最大值或最小值以及相应的点坐标．若不存在请说明理由；
（3）设直线DE与y轴交于点M．当ME=3MD时，请求出抛物线的解析式；
（4）图中的抛物线是动点移动到某一时刻的图象，此时抛物线上是否存在点P，使过点P的直线l平分正方形的面积，且点D和点E到直线l的距离相等？若存在，请在图中画出l和抛物线的所有交点；若不存在，请说明理由．

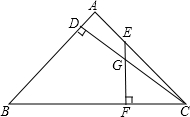10．△ABC中，AB=AC，CD⊥AB于D，E是AC上动点，EF⊥BC于F，交CD于G，若EG=$\frac{1}{2}$CF，则$\frac{BD}{AD}$=$\frac{\sqrt{17}+1}{16}$．

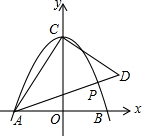9．如图，抛物线y=ax²+4与x轴交于A、B两点（A在B的左边），与y轴交于点C，AB=4．
（1）直接写出抛物线的解析式．   
（2）过点C作CD⊥AC，且CD=AC，连接AD交抛物线于点P，求点P的坐标．