科目： 来源： 题型：选择题

19．如图，在平面直角坐标系系中，直线y=k₁x+2与x轴交于点A，与y轴交于点C，与反比例函数y=$\frac{{k}_{2}}{x}$在第一象限内的图象交于点B，连接BO．若S_△OBC=1，tan∠BOC=$\frac{1}{3}$，则k₂的值是（　　）

A．

-3

B．

1

C．

2

D．

3

科目： 来源： 题型：解答题

18．如图，在平面直角坐标系中，抛物线y=mx²-8mx+4m+2（m＞0）与y轴的交点为A，与x轴的交点分别为B（x₁，0），C（x₂，0），且x₂-x₁=4，直线AD∥x轴，在x轴上有一动点E（t，0）过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q．
（1）求抛物线的解析式；
（2）当0＜t≤8时，求△APC面积的最大值；
（3）当t＞2时，是否存在点P，使以A、P、Q为顶点的三角形与△AOB相似？若存在，求出此时t的值；若不存在，请说明理由．

科目： 来源： 题型：填空题

科目： 来源： 题型：填空题

16．观光塔是潍坊市区的标志性建筑，为测量其高度，如图，一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°，然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°．已知楼房高AB约是45m，根据以上观测数据可求观光塔的高CD是135m．

科目： 来源： 题型：解答题

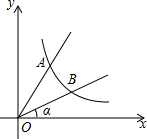15．如图，直线y=2x与反比例函数y=$\frac{k}{x}$（k≠0，x＞0）的图象交于点A（1，a），B是反比例函数图象上一点，直线OB与x轴的夹角为α，tanα=$\frac{1}{2}$．
（1）求k的值．
（2）求点B的坐标．
（3）设点P（m，0），使△PAB的面积为2，求m的值．

科目： 来源： 题型：填空题

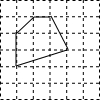14．如图，多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形，它的面积S可用公式S=a+$\frac{1}{2}$b-1（a是多边形内的格点数，b是多边形边界上的格点数）计算，这个公式称为“皮克定理”．现用一张方格纸共有200个格点，画有一个格点多边形，它的面积S=40．
（1）这个格点多边形边界上的格点数b=82-2a（用含a的代数式表示）．
（2）设该格点多边形外的格点数为c，则c-a=118．

科目： 来源： 题型：选择题

13．下列四个图形分别是四届国际数学家大会的会标，其中属于中心对称图形的有（　　）
              

A．

1个

B．

2个

C．

3个

D．

4个

科目： 来源： 题型：解答题

12．如图，已知直线y=x+k和双曲线y=$\frac{k+1}{x}$（k为正整数）交于A，B两点．
（1）当k=1时，求A、B两点的坐标；
（2）当k=2时，求△AOB的面积；
（3）当k=1时，△OAB的面积记为S₁，当k=2时，△OAB的面积记为S₂，…，依此类推，当k=n时，△OAB的面积记为S_n，若S₁+S₂+…+S_n=$\frac{133}{2}$，求n的值．

科目： 来源： 题型：选择题

11．如图，正方形ABCD位于第一象限，边长为3，点A在直线y=x上，点A的横坐标为1，正方形ABCD的边分别平行于x轴、y轴．若双曲线y=$\frac{k}{x}$与正方形ABCD有公共点，则k的取值范围为（　　）

A．

1＜k＜9

B．

2≤k≤34

C．

1≤k≤16

D．

4≤k＜16

科目： 来源： 题型：解答题