科目： 来源： 题型：选择题

14．如图，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE最小，则这个最小值为（　　）

A．

$\sqrt{3}$

B．

2$\sqrt{3}$

C．

2$\sqrt{6}$

D．

$\sqrt{6}$

科目： 来源： 题型：选择题

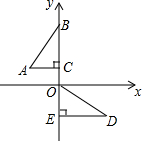13．如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是（　　）

	A．	△ABC绕点C顺时针旋转90°，再向下平移3
	B．	△ABC绕点C顺时针旋转90°，再向下平移1
	C．	△ABC绕点C逆时针旋转90°，再向下平移1
	D．	△ABC绕点C逆时针旋转90°，再向下平移3

科目： 来源： 题型：选择题

12．如图，Rt△ABC中∠C=90°，∠BAC=30°，AB=8，以2$\sqrt{3}$为边长的正方形DEFG的一边GD在直线AB上，且点D与点A重合，现将正方形DEFG沿A-B的方向以每秒1个单位的速度匀速运动，当点D与点B重合时停止，则在这个运动过程中，正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是（　　）

A．

B．

C．

D．

科目： 来源： 题型：解答题

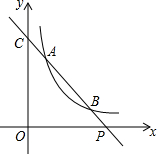11．如图，已知直线y=ax+b与双曲线y=$\frac{k}{x}$（x＞0）交于A（x₁，y₁），B（x₂，y₂）两点（A与B不重合），直线AB与x轴交于P（x₀，0），与y轴交于点C．
（1）若A，B两点坐标分别为（1，3），（3，y₂），求点P的坐标．
（2）若b=y₁+1，点P的坐标为（6，0），且AB=BP，求A，B两点的坐标．
（3）结合（1），（2）中的结果，猜想并用等式表示x₁，x₂，x₀之间的关系（不要求证明）．

科目： 来源： 题型：选择题

10．如图，AD、BC是⊙O的两条互相垂直的直径，点P从点O出发，沿O→C→D→O的路线匀速运动．设∠APB=y（单位：度），那么y关于点P运动的时间x（单位：秒）的函数图象大致是（　　）

A．

B．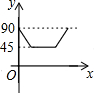

C．

D．

科目： 来源： 题型：选择题

9．将如图所示的几何图形，绕直线l旋转一周得到的立体图形（　　）

A．

B．

C．

D．

科目： 来源： 题型：解答题

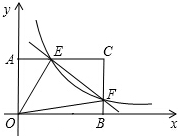8．在矩形AOBC中，OB=6，OA=4，分别以OB，OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系．F是边BC上一点（不与B、C两点重合），过点F的反比例函数y=$\frac{k}{x}$（k＞0）图象与AC边交于点E．
（1）请用k表示点E，F的坐标；
（2）若△OEF的面积为9，求反比例函数的解析式．

科目： 来源： 题型：选择题

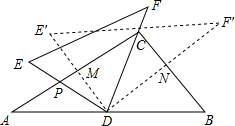7．将一副三角尺（在Rt△ABC中，∠ACB=90°，∠B=60°，在Rt△EDF中，∠EDF=90°，∠E=45°）如图摆放，点D为AB的中点，DE交AC于点P，DF经过点C，将△EDF绕点D顺时针方向旋转α（0°＜α＜60°），DE′交AC于点M，DF′交BC于点N，则$\frac{PM}{CN}$的值为（　　）

A．

$\sqrt{3}$

B．

$\frac{\sqrt{3}}{2}$

C．

$\frac{\sqrt{3}}{3}$

D．

$\frac{1}{2}$

科目： 来源： 题型：解答题

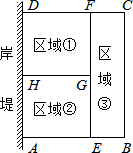6．为了节省材料，某水产养殖户利用水库的岸堤（岸堤足够长）为一边，用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym²．
（1）求y与x之间的函数关系式，并注明自变量x的取值范围；
（2）x为何值时，y有最大值？最大值是多少？

科目： 来源： 题型：选择题