9．阅读下列材料：
2015年清明小长假，北京市属公园开展以“清明踏青，春色满园”为主题的游园活动，虽然气温小幅走低，但游客踏青赏花的热情很高，市属公园游客接待量约为190万人次．其中，玉渊潭公园的樱花、北京植物园的桃花受到了游客的热捧，两公园的游客接待量分别为38万人次、21.75万人次；颐和园、天坛公园、北海公园因皇家园林的厚重文化底蕴与满园春色成为游客的重要目的地，游客接待量分别为26万人次、20万人次、17.6万人次；北京动物园游客接待量为18万人次，熊猫馆的游客密集度较高．
2014年清明小长假，天气晴好，北京市属公园游客接待量约为200万人次，其中，玉渊潭公园游客接待量比2013 年清明小长假增长了25%；颐和园游客接待量为26.2万人次，2013 年清明小长假增加了4.6万人次；北京动物园游客接待量为22万人次．
2013年清明小长假，玉渊潭公园、陶然亭公园、北京动物园游客接待量分别为32万人次、13万人次、14.9 万人次．
根据以上材料解答下列问题：
（1）2014年清明小长假，玉渊潭公园游客接待量为40万人次；
（2）选择统计表或统计图，将2013-2015年清明小长假玉渊潭公园、颐和园和北京动物园的游客接待量表示出来．

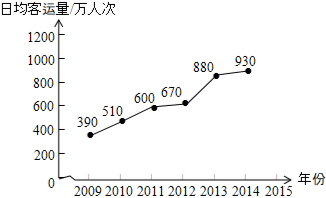8．北京市2009-2014年轨道交通日均客运量统计如图所示．根据统计图中提供的信息，预估2015年北京市轨道交通日均客运量约980万人次，你的预估理由是因为2012-2013年发生数据突变，故参照2013-2014增长进行估算．．

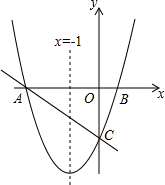7．如图，对称轴为直线x=-1的抛物线y=x²+bx+c与x轴相交于A、B两点，其中点A的坐标为（-3，0）．
（1）求抛物线的解析式；
（2）C为抛物线与y轴的交点，若点P在抛物线上，且S_△POC=4S_△BOC，求点P的坐标．

6．如图1，已知直线y=x+3与x轴交于点A，与y轴交于点B，将直线在x轴下方的部分沿x轴翻折，得到一个新函数的图象（图中的“V形折线”）．
（1）类比研究函数图象的方法，请列举新函数的两条性质，并求新函数的解析式；
（2）如图2，双曲线y=$\frac{k}{x}$与新函数的图象交于点C（1，a），点D是线段AC上一动点（不包括端点），过点D作x轴的平行线，与新函数图象交于另一点E，与双曲线交于点P．
①试求△PAD的面积的最大值；
②探索：在点D运动的过程中，四边形PAEC能否为平行四边形？若能，求出此时点D的坐标；若不能，请说明理由．

5．古希腊数学家把数1，3，6，10，15，21，…叫做三角数，它有一定的规律性．若把第一个三角数记为a₁，第二个三角数记为a₂…，第n个三角数记为a_n，计算a₁+a₂，a₂+a₃，a₃+a₄，…由此推算a₃₉₉+a₄₀₀=1.6×10⁵或160000．

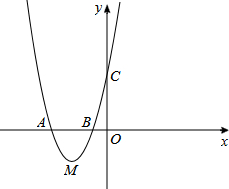4．如图，抛物线经过A（-2，0），B（-$\frac{1}{2}$，0），C（0，2）三点．
（1）求抛物线的解析式；
（2）在直线AC下方的抛物线上有一点D，使得△DCA的面积最大，求点D的坐标；
（3）设点M是抛物线的顶点，试判断抛物线上是否存在点H满足∠AMH=90°？若存在，请求出点H的坐标；若不存在，请说明理由．

3．如图，两个全等的△ABC和△DFE重叠在一起，固定△ABC，将△DEF进行如下变换：
（1）如图1，△DEF沿直线CB向右平移（即点F在线段CB上移动），连接AF、AD、BD．请直接写出S_△ABC与S_{四边形AFBD}的关系；
（2）如图2，当点F平移到线段BC的中点时，若四边形AFBD为正方形，那么△ABC应满足什么条件？请给出证明；
（3）在（2）的条件下，将△DEF沿DF折叠，点E落在FA的延长线上的点G处，连接CG，请你在图3的位置画出图形，并求出sin∠CGF的值．

2．如图，在△ABC中，AB＞AC，点D、E分别是边AB、AC的中点，点F在BC边上，连接DE、DF、EF，则添加下列哪一个条件后，仍无法判断△FCE与△EDF全等（　　）

A．

∠A=∠DFE

B．

BF=CF

C．

DF∥AC

D．

∠C=∠EDF

1．（1）如图1是某个多面体的表面展开图．
①请你写出这个多面体的名称，并指出图中哪三个字母表示多面体的同一点；
②如果沿BC、GH将展开图剪成三块，恰好拼成一个矩形，那么△BMC应满足什么条件？（不必说理）
（2）如果将一个三棱柱的表面展开图剪成四块，恰好拼成一个三角形，如图2，那么该三棱柱的侧面积与表面积的比值是多少？为什么？（注：以上剪拼中所有接缝均忽略不计）

20．清明期间，某校师生组成200个小组参加“保护环境，美化家园”植树活动．综合实际情况，校方要求每小组植树量为2至5棵，活动结束后，校方随机抽查了其中50个小组，根据他们的植树量绘制出如图所示的两幅不完整统计图．请根据图中提供的信息，解答下面的问题：

（1）请把条形统计图补充完整，并算出扇形统计图中，植树量为“5棵树”的圆心角是72°．
（2）请你帮学校估算此次活动共种多少棵树．