
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
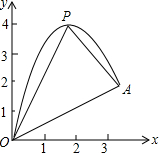 如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=-x2+4x刻画,斜坡可以用一次函数y=$\frac{1}{2}$x刻画.
如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数y=-x2+4x刻画,斜坡可以用一次函数y=$\frac{1}{2}$x刻画.查看答案和解析>>
科目: 来源: 题型:解答题
 如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.
如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
 如图,在Rt△ABC中,AB=BC,∠B=90°,AC=10$\sqrt{2}$.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是25.
如图,在Rt△ABC中,AB=BC,∠B=90°,AC=10$\sqrt{2}$.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积是25.查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com