科目： 来源： 题型：选择题

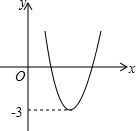6．已知函数y=ax²+bx+c的图象如图所示，那么关于x的方程ax²+bx+c+1=0的根的情况是（　　）

	A．	无实数根		B．	有两个相等实数根
	C．	有两个异号实数根		D．	有两个同号不等实数根

科目： 来源： 题型：选择题

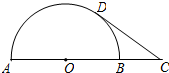5．如图，AB是半圆的直径，点O是圆心，点C是AB延长线的一点，CD与半圆相切于点D．若AB=6，CD=4，则sin∠C的值为（　　）

A．

$\frac{3}{4}$

B．

$\frac{3}{5}$

C．

$\frac{4}{5}$

D．

$\frac{2}{3}$

科目： 来源： 题型：填空题

科目： 来源： 题型：选择题

3．如图，OA是北偏东30°方向的一条射线，若射线OB与射线OA垂直，则OB的方向角是（　　）

A．

西偏北30°

B．

北偏西60°

C．

北偏东30°

D．

东偏北60°

科目： 来源： 题型：选择题

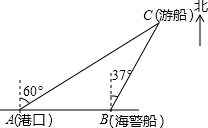2．一艘观光游船从港口A以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以每小时40海里的速度前往救援，则海警船到达事故船C处所需的时间大约为（单位：小时）（　　）

A．

$\frac{1}{sin37°}$

B．

$\frac{1}{cos37°}$

C．

sin37°

D．

cos37°

科目： 来源： 题型：选择题

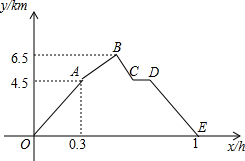1．从甲地到乙地，先是一段平路，然后是一段上坡路，小明骑车从甲地出发，到达乙地后立即返回甲地，途中休息了一段时间，假设小明骑车在平路、上坡、下坡时分别保持匀速前进，已知小明骑车上坡的速度比在平路上的速度每小时少5km．下坡的速度比在平路上的速度每小时多5km．设小明出发xh后，到达离甲地ykm的方，图中的折线OABCDE 表示y与x之间的函数关系，有下列说法正确的有（　　）个
①小明骑车在平路上的速度为15km/h；
②小明途中休息了0.1h；
③如果小明两次经过途中某一地点的时间间隔为0.15h，那么该地点离甲地5.75km．

A．

0

B．

1

C．

2

D．

3

科目： 来源： 题型：填空题

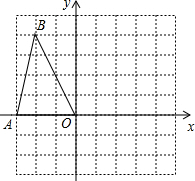20．如图，正方形网格中的每一个小正方形的边长都是1，△AOB的三个顶点都在格点上，以O为坐标原点，建立如图平面直角坐标系，若把△AOB绕着点O顺时针旋转90°，得到△A₁OB₁，则点B旋转后的对应点B₁的坐标为（4，2）．

科目： 来源： 题型：解答题

19．已知，四边形ABCD是正方形，点F是边AB、BC上一动点，DE⊥DF，且DE=DF，M为EF的中点．
（1）当点F在边AB上时，（如图①）．
①求证：点E在直线BC上；
②若BF=2，则MC的长为$\sqrt{2}$；
（2）当点F在BC上时，（如图②），求$\frac{BF}{CM}$的值．

科目： 来源： 题型：选择题

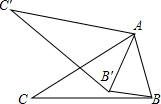18．如图所示，在△ABC中，∠CAB=70°，现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′，连接BB′，若BB′∥AC′，则∠CAB′的度数为（　　）

A．

20°

B．

25°

C．

30°

D．

40°

科目： 来源： 题型：解答题