
科目: 来源: 题型:选择题
| A. | (-4,5) | B. | (-4,-1) | C. | (2,-1) | D. | (2,5) |
查看答案和解析>>
科目: 来源: 题型:解答题
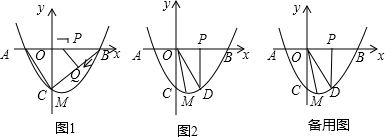
查看答案和解析>>
科目: 来源: 题型:解答题
 某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量的$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量的$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.查看答案和解析>>
科目: 来源: 题型:解答题
 如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.查看答案和解析>>
科目: 来源: 题型:解答题
| 甲种品牌化妆品 | 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 6 | 12 | 6 |
| 乙种品牌化妆品 | 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 12 | 6 | 12 |
查看答案和解析>>
科目: 来源: 题型:解答题

| 组别 | 雾霾天气的主要成因 | 百分比 |
| A | 工业污染 | 45% |
| B | 汽车尾气排放 | m |
| C | 炉烟气排放 | 15% |
| D | 其他(滥砍滥伐等) | n |
查看答案和解析>>
科目: 来源: 题型:填空题
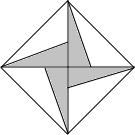 如图,正方形的阴影部分是由四个直角边长都是1和3的直角三角形组成的,假设可以在正方形内部随意取点,那么这个点取在阴影部分的概率为$\frac{1}{3}$.
如图,正方形的阴影部分是由四个直角边长都是1和3的直角三角形组成的,假设可以在正方形内部随意取点,那么这个点取在阴影部分的概率为$\frac{1}{3}$.查看答案和解析>>
科目: 来源: 题型:选择题
 如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( )
如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
查看答案和解析>>
科目: 来源: 题型:选择题
 如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是( )
如图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是( )| A. | (4,2) | B. | (4,1) | C. | (5,2) | D. | (5,1) |
查看答案和解析>>
科目: 来源: 题型:选择题
 云南鲁甸发生地震后,某社区开展献爱心活动,社区党员积极向灾区捐款,如图是该社区部分党员捐款情况的条形统计图,那么本次捐款钱数的众数和中位数分别是( )
云南鲁甸发生地震后,某社区开展献爱心活动,社区党员积极向灾区捐款,如图是该社区部分党员捐款情况的条形统计图,那么本次捐款钱数的众数和中位数分别是( )| A. | 100元,100元 | B. | 100元,200元 | C. | 200元,100元 | D. | 200元,200元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com