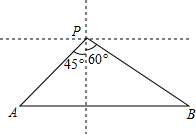12．如图，一海伦位于灯塔P的西南方向，距离灯塔40$\sqrt{2}$海里的A处，它沿正东方向航行一段时间后，到达位于灯塔P的南偏东60°方向上的B处，求航程AB的值（结果保留根号）．

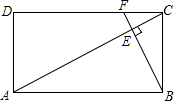11．如图，矩形ABCD中，F是DC上一点，BF⊥AC，垂足为E，$\frac{AD}{AB}$=$\frac{1}{2}$，△CEF的面积为S₁，△AEB的面积为S₂，则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{1}{16}$．

10．如图，在⊙O中，半径OD垂直于弦AB，垂足为C，OD=13cm，AB=24cm，则CD=8cm．

9．甲乙两人8次射击的成绩如图所示（单位：环）根据图中的信息判断，这8次射击中成绩比较稳定的是甲（填“甲”或“乙”）

8．在20km越野赛中，甲乙两选手的行程y（单位：km）随时间x（单位：h）变化的图象如图所示，根据图中提供的信息，有下列说法：①两人相遇前，甲的速度小于乙的速度；②出发后1小时，两人行程均为10km；③出发后1.5小时，甲的行程比乙多3km；④甲比乙先到达终点．其中正确的有（　　）

A．

1个

B．

2个

C．

3个

D．

4个

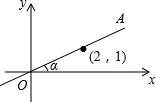7．如图，在平面直角坐标系中，直线OA过点（2，1），则tanα的值是（　　）

A．

$\frac{\sqrt{5}}{5}$

B．

$\sqrt{5}$

C．

$\frac{1}{2}$

D．

2

6．下面四个几何体中，俯视图是圆的几何体共有（　　）

A．

1个

B．

2个

C．

3个

D．

4个

5．方程x²+m=0有实数根的条件是（　　）

A．

m＞0

B．

m≥0

C．

m＜0

D．

m≤0

4．如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，将∠QPN绕点P旋转，旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C，D不重合）．
（1）如图①，当α=90°时，DE，DF，AD之间满足的数量关系是DE+DF=AD；
（2）如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE+DF=$\frac{1}{2}$AD，请给出证明；
（3）在（2）的条件下，若旋转过程中∠QPN的边PQ与射线AD交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．

3．阅读下列材料，并解决相关的问题．
按照一定顺序排列着的一列数称为数列，排在第一位的数称为第1项，记为a₁，依此类推，排在第n位的数称为第n项，记为a_n．
一般地，如果一个数列从第二项起，每一项与它前一项的比等于同一个常数，那么这个数列叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母q表示（q≠0）．如：数列1，3，9，27，…为等比数列，其中a₁=1，公比为q=3．
则：（1）等比数列3，6，12，…的公比q为2，第4项是24．
（2）如果一个数列a₁，a₂，a₃，a₄，…是等比数列，且公比为q，那么根据定义可得到：$\frac{a_2}{a_1}$=q，$\frac{a_3}{a_2}$=q，$\frac{a_4}{a_3}$=q，…$\frac{a_n}{{{a_{n-1}}}}$=q．
所以：a₂=a₁•q，a₃=a₂•q=（a₁•q）•q=a₁•q²，a₄=a₃•q=（a₁•q²）•q=a₁•q³，…
由此可得：a_n=a₁•q^n-1（用a₁和q的代数式表示）．
（3）若一等比数列的公比q=2，第2项是10，请求它的第1项与第4项．