
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
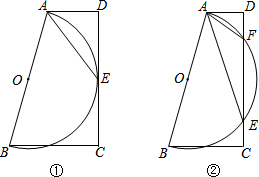 在梯形ABCD中,AD∥BC,∠D=90°,以AB为直径作⊙O.
在梯形ABCD中,AD∥BC,∠D=90°,以AB为直径作⊙O.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
 胡老师散步途径A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东45°方向,在B地正北方向,在C地北偏西60°方向,C地在A地北偏东75°方向,B、D两地相距2km.问奥运圣火从A地传到D地的路程(即A→B→C→D的路程)大约是多少?(最后结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
胡老师散步途径A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东45°方向,在B地正北方向,在C地北偏西60°方向,C地在A地北偏东75°方向,B、D两地相距2km.问奥运圣火从A地传到D地的路程(即A→B→C→D的路程)大约是多少?(最后结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目: 来源: 题型:填空题
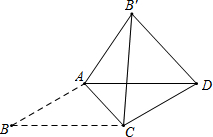 如图,平行四边形ABCD中,∠B=30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D,若AB=2$\sqrt{3}$,∠AB′D=75°,则:①∠CB′D=45°;②BC=3$+\sqrt{3}$.
如图,平行四边形ABCD中,∠B=30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D,若AB=2$\sqrt{3}$,∠AB′D=75°,则:①∠CB′D=45°;②BC=3$+\sqrt{3}$.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com