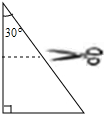10．如图所示，是一张直角三角形纸片，其中有一个内角为30°，最小边长为2，点D、E分别是一条直角边和斜边的中点，先将纸片沿DE剪开，然后再将两部分拼成一个四边形，则所得四边形的周长是8或4+2$\sqrt{3}$．

9．如图1是一个拱形桥，该拱形桥及河道截面的示意图如图2所示，该示意图由抛物线的一部分ABC（B是该抛物线的顶点）和矩形的三边AO，OD，CD组成．已知河底OD是水平的，OD=10米，CD=8米，点B到河底的距离是A到河底的距离的1.5倍．以OD所在的直线为x轴，OA所在的直线为y轴建立平面直角坐标系．
（1）求点B的坐标及抛物线的解析式；
（2）一行人走在该拱形桥上面，帽子（点M）不小心掉进了河里（漂在河面上），该行人在A处用一根2.5米长的木棍恰好能钩到距离点E1.5米的帽子，求此时河水的高度；
（3）已知从某时刻开始的36小时内，水面与河底的距离h（米）随时间t（小时）的变化满足函数关系h=-$\frac{1}{128}$（t-17）²+9（0≤t≤36），且当水面到顶点B的距离不大于5米时，需禁止船只通行，求在这段时间内，需要多长时间禁止船只通行？

8．如图，将一张正六边形纸片的阴影部分剪下，拼成一个四边形，若拼成的四边形的面积为2a，则纸片的剩余部分的面积为 （　　）

A．

5a

B．

4a

C．

3a

D．

2a

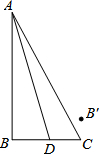7．如图，已知∠B=90°，AB=3cm，BC=$\sqrt{3}$cm，点D是线段BC上的一个动点，连接AD，动点B′始终与点B关于直线AD对称，当点D由点B位置向右运动至点C位置时，相应的点B′所经过的路程为（　　）

A．

3cm

B．

πcm

C．

2$\sqrt{3}$cm

D．

2πcm

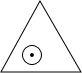6．如图，一个半径为1的圆形纸片在边长为a（a≥2$\sqrt{3}$）的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（　　）

A．

$\frac{π}{3}$

B．

$\frac{3\sqrt{3}-π}{3}$

C．

3$\sqrt{3}$-π

D．

不能求出具体值

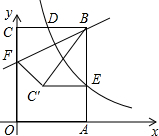5．如图，直角坐标系中，矩形OABC的顶点O与原点重合，顶点A、C分别在x轴、y轴的正半轴上，若点B的坐标为（4，6），双曲线y=$\frac{k}{x}$（x＞0）的图象经过BC的中点D，与AB交于点E，F为OC边上一点，把△BCF沿直线BF翻折，使点C落在点C′处（C′在矩形OABC内部），且C′E∥BC，则CF的长为$\frac{16-4\sqrt{7}}{3}$．

4．我们知道平行四边形有很多性质．现在如果我们把平行四边形沿着它的一条对角线翻折．会发现这其中还有更多的结论，如图，已知平行四边形ABCD中，∠B=30°，AB≠BC，将△ABC沿AC翻折至△AB′C，连接B′D．
【发现与证明】：如图1：求证：①△AGC是等腰三角形；②B′D∥AC
【应用与解答】：如图2：如果AB=2$\sqrt{3}$，BC=1，AB′与CD相交于点E，求△AEC的面积
【拓展与探索】：如果AB=2$\sqrt{3}$，当BC的长为多少时，△AB′D是直角三角形？

3．（阅读）如图1，在平面直角坐标系xOy中，已知点A（a、O）（a＞0），B（2，3），C（0，3）．过原点O作直线l，使它经过第一、第三象限，直线l与y轴的正半轴所成角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ[θ，a]．
【理解】若点D与点A重合，则这个操作过程为FZ[45°，3]；直接写出答案
【尝试】
（1）若点D恰为AB的中点（如图2），求θ；
（2）经过FZ[45°，a]操作，点B落在点E处，若点E在四边形0ABC的边AB上，求出a的值；若点E落在四边形0ABC的外部，直接写出a的取值范围；

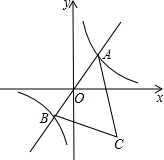2．如图，已知A是双曲线y=$\frac{7}{x}$在第一象限的分支上一个动点，连接AO并延长另一分支于点B，以AB为一边作等边△ABC，点C在第四象限，随着点A的运动，点C的位置也不断发生变化，但点C始终在双曲线y=$\frac{k}{x}$（k＜0）上运动，则k的值是-21．

1．如图，已知矩形OABC的一个顶点B的坐标是（4，2），反比例函数y=$\frac{k}{x}$（x＞0）的图象经过OB的中点E，且与边BC交于点D．
（1）求反比例函数的解析式和点D的坐标；
（2）求三角形DOE的面积；
（3）若过点D的直线y=mx+n将矩形OABC的面积分成3：5的两部分，求此直线解析式．