16．已知反比例函数y=-$\frac{3m}{x}$和一次函数y=-kx-1的图象都经过点P（m，-3m），求点P的坐标以及反比例函数和一次函数关系式．

15．问题背景：某课外学习小组在一次学习研讨中，得到了如下两个命题：
①如图a，在正三角形ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON=60°，则BM=CN；
②如图b，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON=90°，则BM=CN；
然后运用类比的思想提出了如下命题：
③如图c，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON=108°，则BM=CN；
任务要求：
（1）请你从①，②，③三个命题中选择一个进行证明；（说明选①做对的得4分，选②做对的得3分，选③做对的得5分）
（2）请你继续完成下面的探索：
ⅰ、如图d，在正n（n≥3）边形ABCDEF…中，M、N分别是CD、DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM=CN成立？（不要求证明）
ⅱ、如图e，在正五边形ABCDE中，M、N分别是DE、AE上的点，BM与CN相交于点O，若∠BON=108° 时，试问结论BM=CN是否还成立？若成立，请给予证明；若不成立．请说明理由．

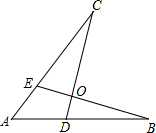14．如图．下面四个条件中，请你选出三个，以其中两个为已知条件，另一个为求证，编一道题并证明（只需写出一种情况）．①AE=AD；②AB=AC；③OB=OC；④∠B=∠C．
已知：AE=AD，AC=AB
求证：∠B=∠C．
证明：

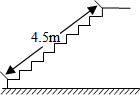13．某中学要修建一座图书楼，为改善安全性能，把楼梯的倾斜角由原来设计的45°改为30°．已知原来设计的楼梯长为4.5m，在楼梯高度不变的情况下，调整后的楼梯多占地面$\frac{9\sqrt{6}-9\sqrt{2}}{4}$m．

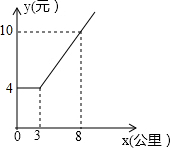12．某市出租车公司收费标准如图所示，
（1）求当x＞3时y与x之间的函数关系式．
（2）如果小明乘此出租车最远能到达13千米处，计算他最多只有多少元钱．

11．已知：AB=AC，AD=AE，BD=CE，求证：∠BAC=∠DAE．

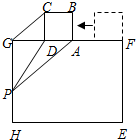10．如图，正方形ABCD的边AD与矩形EFGH的边FG重合，将正方形ABCD以lcm/s的速度沿FG方向移动，移动开始前点A与点F重合．在移动过程中，边 AD始终与边FG重合，连接CG，过点A作CG的平行线交线段GH于点P，连接PD．已知正方形ABCD的边长为lcm，矩形EFGH的边FG、GH的长分别为4cm、3cm．设正方形移动时间为x（s），线段GP的长为y （cm），其中0≤x≤2.5．
（1）试求出y关于x的函数关系式，并求当y=3时相应x的值；
（2）记△DGP的面积为S₁，ACDG的面积为S₂，试说明S₁-S₂是常数．

9．AB是⊙O的一条弦，它的中点为M，过点M作一条非直径的弦CD，过点C和D作⊙O的两条切线，分别与直线AB相交于P、Q两点．求证：PA=QB．

8．在实数范围内定义运算“※”，其法则为：a※b=4ab，例如：2※6=4×2×6=48．
（1）求3※7的值；
（2）求x※x+8※x+2※8=0中x的值．

7．某食品店只有一台不等臂的天平和一只1kg的砝码．一名顾客欲购买2kg糖果，售货员先将砝码置左盘，糖果置右盘，平衡后，将此次称得的糖果给顾客，再将砝码置右盘，糖果置左盘，平衡后，又将第二次称得的糖果给顾客．试问：这种称法便宜了谁？