11.在进行二次根式的化简与运算时,如遇到$\frac{3}{\sqrt{5}}$,$\sqrt{\frac{2}{3}}$,$\frac{2}{\sqrt{3}+1}$这样的式子,还需做进一步的化简:
$\frac{3}{\sqrt{5}}$=$\frac{3×\sqrt{5}}{\sqrt{5}×\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$.①
$\sqrt{\frac{2}{3}}$=$\sqrt{\frac{2×3}{3×3}}$=$\frac{\sqrt{6}}{3}$.②
$\frac{2}{\sqrt{3}+1}$=$\frac{2×(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}$=$\frac{2(\sqrt{3}-1)}{(\sqrt{3})^{2}-{1}^{2}}$=$\sqrt{3}$-1.③
以上化简的步骤叫做分母有理化.
$\frac{2}{\sqrt{3}+1}$还可以用以下方法化简:
$\frac{2}{\sqrt{3}+1}$=$\frac{3-1}{\sqrt{3}+1}$=$\frac{(\sqrt{3})^{2}-1}{\sqrt{3}+1}$=$\frac{(\sqrt{3}+1)(\sqrt{3}-1)}{\sqrt{3}+1}$=$\sqrt{3}$-1.④
(Ⅰ)请用不同的方法化简$\frac{2}{\sqrt{5}+\sqrt{3}}$
(1)参照③式化简$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-$\sqrt{3}$
(2)参照④式化简$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-$\sqrt{3}$
(Ⅱ)化简:$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+…+$\frac{1}{\sqrt{2n+1}+\sqrt{2n-1}}$.

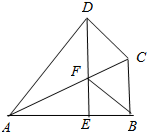 如图,四边形ABCD是筝形,且AB=8,BC=4,∠ABC=90°,过D作DE⊥AB交AC于点F,连接BF.求证:DF=CD,并判断四边形BCDF的形状.
如图,四边形ABCD是筝形,且AB=8,BC=4,∠ABC=90°,过D作DE⊥AB交AC于点F,连接BF.求证:DF=CD,并判断四边形BCDF的形状.