
科目: 来源: 题型:选择题
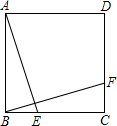 如图,E,F分别是正方形ABCD的边BC,CD上的点,且BE=CF,连接AE,BF,将△ABE绕正方形的中心按逆时针方向旋转α(0<α<180°)到∠BCF,则旋转角α等于( )
如图,E,F分别是正方形ABCD的边BC,CD上的点,且BE=CF,连接AE,BF,将△ABE绕正方形的中心按逆时针方向旋转α(0<α<180°)到∠BCF,则旋转角α等于( )| A. | 90° | B. | 60° | C. | 45° | D. | 120° |
查看答案和解析>>
科目: 来源: 题型:解答题
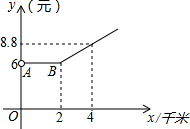 某市的出租车收费y(元)与路程x(千米)之间的函数关系如图所示.
某市的出租车收费y(元)与路程x(千米)之间的函数关系如图所示.查看答案和解析>>
科目: 来源: 题型:解答题
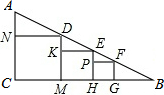 如图,在Rt△ABC中,∠C=90°,从左向右依次作正方形CNDM,正方形MKEH,正方形HPFG.已知正方形CNDM的边长为10,正方形MKEH的边长为8.
如图,在Rt△ABC中,∠C=90°,从左向右依次作正方形CNDM,正方形MKEH,正方形HPFG.已知正方形CNDM的边长为10,正方形MKEH的边长为8.查看答案和解析>>
科目: 来源: 题型:解答题
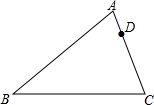 如图,已知在△ABC中,AB=14,BC=12,AC=10,D是AC上一点,且AD=4,过点D画一条直线l,把△ABC分成两部分,使其中的一个三角形与△ABC相似,请在图中画出所有符合要求的直线l,并写出所作三角形与△ABC的相似比.
如图,已知在△ABC中,AB=14,BC=12,AC=10,D是AC上一点,且AD=4,过点D画一条直线l,把△ABC分成两部分,使其中的一个三角形与△ABC相似,请在图中画出所有符合要求的直线l,并写出所作三角形与△ABC的相似比.查看答案和解析>>
科目: 来源: 题型:解答题
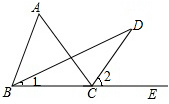 阅读下面的证明过程,在括号内补充推理的依据.
阅读下面的证明过程,在括号内补充推理的依据.查看答案和解析>>
科目: 来源: 题型:解答题
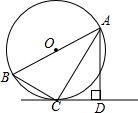 如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,AD垂直于过C点的⊙O的切线于点D.
如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,AD垂直于过C点的⊙O的切线于点D.查看答案和解析>>
科目: 来源: 题型:解答题
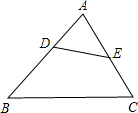 如图,D、E分别为△ABC的边AB、AC上的点,且∠ADE=∠ACB.
如图,D、E分别为△ABC的边AB、AC上的点,且∠ADE=∠ACB.查看答案和解析>>
科目: 来源: 题型:解答题
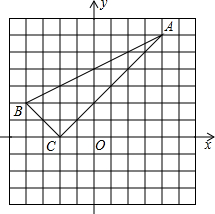 如图,已知△ABC的三个顶点的坐标分别为A(4,6),B(-4,2),C(-2,0).
如图,已知△ABC的三个顶点的坐标分别为A(4,6),B(-4,2),C(-2,0).查看答案和解析>>
科目: 来源: 题型:解答题
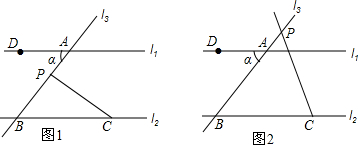
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com