科目： 来源： 题型：填空题

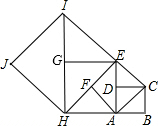10．如图，如果以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去…，已知正方形ABCD的面积S₁为1，按上述方法所作的正方形的面积依次为S₂，S₃，…，S_n（n为正整数），那么第2015个正方形的面积S₂₀₁₅为2²⁰¹⁴．

科目： 来源： 题型：填空题

科目： 来源： 题型：填空题

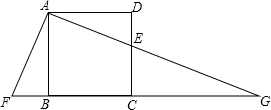8．如图，E是正方形ABCD的边DC上的一点，过点A作AF⊥AE，交CB的延长线于点F，AE的延长线交BC的延长线于点G．若AF=13，DE=5，则CG的长是$\frac{84}{5}$．

科目： 来源： 题型：选择题

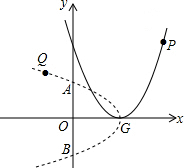7．如图，点P为抛物线y=x²-4x+4上任一点，将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点（点A在点B的上方），点Q为点P旋转后的对应点．若点P的横坐标为4时，则Q点的坐标为（　　）

A．

（-2，3）

B．

（-2，2$\sqrt{2}$）

C．

（-2，2）

D．

（1+$\frac{\sqrt{2}}{2}$，2）

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

4．如图①所示，直线L：y=mx+5m与x轴负半轴，y轴正半轴分别交于A、B两点．

（1）当OA=OB时，求点A坐标及直线L的解析式；
（2）在（1）的条件下，如图②所示，设Q为AB延长线上一点，作直线OQ，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若AM=$\sqrt{17}$，求BN的长；
（3）当m取不同的值时，点B在y轴正半轴上运动，分别以OB、AB为边，点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE，连EF交y轴于P点，如图③．
问：当点B在y轴正半轴上运动时，试猜想PB的长是否为定值？若是，请求出其值；若不是，说明理由．

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

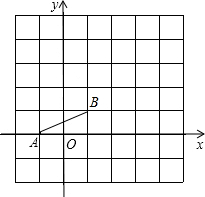2．如图，已知A（-1，0），B（1，1），把线段AB平移，使点B移动到点D（3，4）处，这时点A移动到点C处．
（1）写出点C的坐标（1，3）；
（2）求经过C、D的直线与y轴的交点坐标．

科目： 来源： 题型：解答题