
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 任意一个负实数的绝对值都是它的相反数 | |
| B. | 任意一个实数都有相反数 | |
| C. | 任意一个实数都有倒数 | |
| D. | 任意一个实数都可以在数轴上找到一点与其对应 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
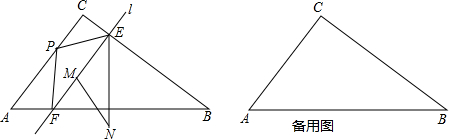
 如图,△ABC中,AB=BC=5,AC=6,过点A作AD∥BC,点P、Q分别是射线AD、线段BA上的动点(不与A、B重合),且AP=BQ,过点P作PE∥AC交线段AQ于点O,连接PQ,设△POQ面积为y,AP=x.
如图,△ABC中,AB=BC=5,AC=6,过点A作AD∥BC,点P、Q分别是射线AD、线段BA上的动点(不与A、B重合),且AP=BQ,过点P作PE∥AC交线段AQ于点O,连接PQ,设△POQ面积为y,AP=x.查看答案和解析>>
科目: 来源: 题型:解答题
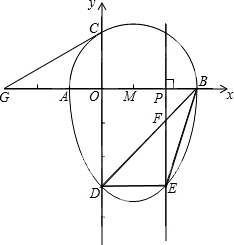 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.“蛋圆”被平行于y轴的直线截得的最大弦长6.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.“蛋圆”被平行于y轴的直线截得的最大弦长6.查看答案和解析>>
科目: 来源: 题型:解答题
| 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| +15 | +10 | 0 | +20 | +15 | +10 | +14 |
| -8 | -12 | -19 | -10 | -9 | -11 | -8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com