练习册

  • 练习册
  • 试题
    相关习题
     0  310739  310747  310753  310757  310763  310765  310769  310775  310777  310783  310789  310793  310795  310799  310805  310807  310813  310817  310819  310823  310825  310829  310831  310833  310834  310835  310837  310838  310839  310841  310843  310847  310849  310853  310855  310859  310865  310867  310873  310877  310879  310883  310889  310895  310897  310903  310907  310909  310915  310919  310925  310933  366461 

    科目： 来源： 题型：填空题

    12．写出一个解为1和2的一元二次方程：x2-3x+2=0．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    11．有一组数据如下：3，a，4，6，7，它们的平均数是5，那么这组数据的方差是（　　）
    A．$\sqrt{2}$B．2C．$\sqrt{10}$D．10

    查看答案和解析>>

    科目： 来源： 题型：选择题

    10．一组数据5，2，5，3，2.5，5，5，5.5，这7个数据的众数和中位数分别是（　　）
    A．5.5，5B．5，5C．5，4D．5，3

    查看答案和解析>>

    科目： 来源： 题型：解答题

    9．选择适当的方法解一元二次方程：
    （1）x2+2x-15=0
    （2）4x-6=（3-2x）x．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    8．数学实验室：制作4张全等的直角三角形纸片（如图1），把这4张纸片拼成以弦长c为边长的正方形构成“弦图”（如图2），古代数学家利用“弦图”验证了勾股定理．

    探索研究：
    （1）小明将“弦图”中的2个三角形进行了旋转，得到图3，请利用图3证明勾股定理；
    数学思考：
    （2）小芳认为用其它的方法改变“弦图”中某些三角形的位置，也可以证明勾股定理．请你想一种方法支持她的观点（先在备用图中补全图形，再予以证明）．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    7．如图，在安大公路（直线BD）的同侧有两个气象信息采集点A、E，点A、E到安大公路的距离AB=12、ED=3，两垂足间的距离BD=20．
    （1）在线段BD上找一点C，铺设线路AC、CE，要使AC+CE最小，请在图中作出点C；
    （2）求出AC+CE的最小值．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    6．如图，已知AD是△ABC的高，且BD=AD，点E在AC上，连结BE交AD于点F，且FD=CD．判断线段BF、AC的数量关系和位置关系，并说明理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    5．图1、图2分别是10×8的网格，网格中每个小正方形的边长均为1，A、B两点在小正方形的顶点上，请在图1、图2中各取一点C（点C必须在小正方形的顶点上），使以A、B、C为顶点的三角形分别满足以下要求：
    （1）在图1中画一个△ABC，使△ABC为面积为10的锐角三角形；
    （2）在图2中画一个△ABC，使△ABC为含有钝角的等腰三角形．

    查看答案和解析>>

    科目： 来源： 题型：解答题

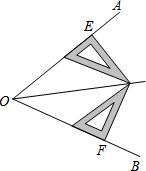    4．用两只完全相同的三角尺在∠AOB的内部如图摆放，两只三角尺较短的直角边必须分别与∠AOB的两边重合，且含30°角的顶点恰好也重合于点C．则射线OC即为∠AOB的角平分线．试利用所学知识说明射线OC平分∠AOB的理由．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    3．如图，已知Rt△ABC中，∠ACB=90°，BC=12，AC=16，CD⊥AB于点D．求CD的长．

    查看答案和解析>>

    同步练习册答案