10．如图，在△ABC中，∠C=90°，∠BAC=70°，将△ABC绕点A顺时针旋转70°，B、C旋转后的对应点分别是B′和C′，连接BB′，则∠BB′C′的度数是（　　）

A．

35°

B．

40°

C．

45°

D．

50°

9．已知△ABC中，AC=6cm，BC=8cm，AB=10cm，CD为AB边上的高．动点P从点A出发，沿着△ABC的三条边逆时针走一圈回到A点，速度为2cm/s，设运动时间为ts．
（1）求CD的长；
（2）t为何值时，△ACP为等腰三角形？
（3）若M为BC上一动点，N为AB上一动点，是否存在M，N使得AM+MN的值最小？如果有请求出最小值，如果没有请说明理由．

8．如图，矩形纸片ABCD中，AB=6，AD=10，点P是边BC上的动点，现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别为E、F，要使折痕始终与边AB、AD有交点，则BP的取值范围是2≤x≤6．

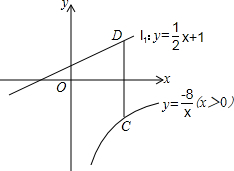7．阅读理解：对于任意正实数a、b，∵${（\sqrt{a}-\sqrt{b}）^2}$≥0，∴a-2$\sqrt{ab}$+b≥0，∴a+b≥2$\sqrt{ab}$，只有当a=b时，等号成立．
结论：在a+b≥2$\sqrt{ab}$（a、b均为正实数）中，若ab为定值p，则a+b≥2$\sqrt{p}$，只有当a=b时，a+b有最小值2$\sqrt{p}$．   根据上述内容，回答下列问题：
（1）若m＞0，只有当m=1时，m+$\frac{1}{m}$有最小值2；
（2）若m＞0，只有当m=2时，2m+$\frac{8}{m}$有最小值8；
（3）已知直线L₁：y=$\frac{1}{2}$x+1，若点C为双曲线y=-$\frac{8}{x}$上任意一点，作CD∥y轴交直线L₁于点D，求线段CD长的最小值及此时C、D点的坐标．

6．（1）计算：$\sqrt{3}$tan30°-（π-2012）⁰-|1-$\sqrt{2}}$|．
（2）解方程：$\frac{2}{x-3}$=$\frac{3}{x}$．

5．写出x＜$\sqrt{7}$的正整数解1，2．

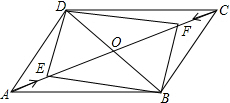4．如图，在平行四边形ABCD中，角线AC、BD相交于点O，动点E以1个单位每秒的速度从点A出发沿AC向运动，点F同时以1个单位每秒的速度从点C发沿CA方向运动，若AC=12，BD=8，求出经过几秒后，四边形BPDQ是矩形？

3．计算边长为3的等边三角形外接圆半径为和圆心到边的距离．

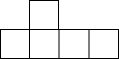2．张明同学设计了某个产品的正方体包装盒如图所示，由于粗心少设计了其中一个顶盖，请你把它补上，使其成为一个两面均有盖的正方体盒子．
（1）共有4种弥补方法；
（2）任意画出一种成功的设计图（在图中补充）；
（3）在你帮忙设计成功的图中，要把-8，10，-12，8，-10，12这些数字分别填入六个小正方形，使得折成的正方体相对面上的两个数相加得0．（直接在图中填上）

1．将一个正方体的表面沿某些棱展开，能展开成的平面图形为（　　）

A．

B．

C．

D．