
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:解答题
 阅读下列材料,完成相关问题:
阅读下列材料,完成相关问题:查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
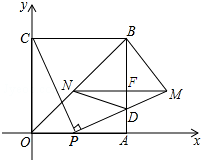 如图,四边形OABC是边长为2的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.
如图,四边形OABC是边长为2的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND、BM,设OP=t.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
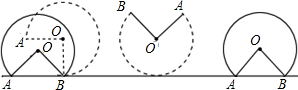
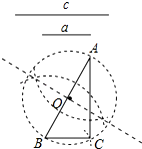 数学课上,老师提出如下问题:已知线段a、c,用尺规作图求作直角三角形ABC,使其斜边AB=c,一条直角边BC=a.小明设计了如下的作图步骤:
数学课上,老师提出如下问题:已知线段a、c,用尺规作图求作直角三角形ABC,使其斜边AB=c,一条直角边BC=a.小明设计了如下的作图步骤:| A. | 勾股定理 | B. | 直径所对的圆周角是直角 | ||
| C. | 勾股定理的逆定理 | D. | 90°的圆周角所对的弦是直径 |
查看答案和解析>>
科目: 来源: 题型:解答题
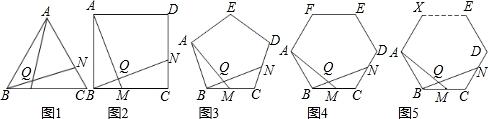
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com