
科目: 来源: 题型:解答题
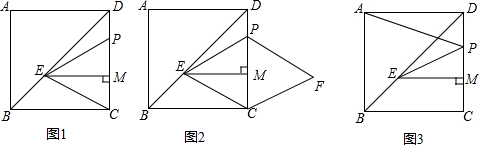
查看答案和解析>>
科目: 来源: 题型:解答题
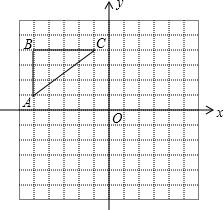 如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:
如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:查看答案和解析>>
科目: 来源: 题型:填空题
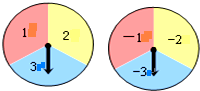 如图,有转盘A、B分别被分成三个面积相等的扇形,上面分别写有3个数字,用力转动两个转盘,转盘上的指针分别指向一个数字,则两个转盘指针指向的两个数之和恰好为0的概率是$\frac{1}{3}$.
如图,有转盘A、B分别被分成三个面积相等的扇形,上面分别写有3个数字,用力转动两个转盘,转盘上的指针分别指向一个数字,则两个转盘指针指向的两个数之和恰好为0的概率是$\frac{1}{3}$.查看答案和解析>>
科目: 来源: 题型:填空题
 如图,某一时刻一根2米长的竹竿EF影长GE为1.2米,此时,小红测得一棵被风吹斜的杨树与地面成30°角,树顶端B在地面上的影子点D与B到垂直地面的落点C的距离是3.6米,则树长AB等于12米.
如图,某一时刻一根2米长的竹竿EF影长GE为1.2米,此时,小红测得一棵被风吹斜的杨树与地面成30°角,树顶端B在地面上的影子点D与B到垂直地面的落点C的距离是3.6米,则树长AB等于12米.查看答案和解析>>
科目: 来源: 题型:解答题
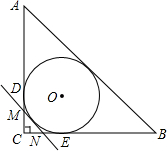 如图,Rt△ABC的内切圆⊙O与两直角边AC、BC分别相切于点D、E,MN切⊙O于点P,分别交CD、CE于点M、N,⊙O的半径为r,求Rt△CMN的周长.
如图,Rt△ABC的内切圆⊙O与两直角边AC、BC分别相切于点D、E,MN切⊙O于点P,分别交CD、CE于点M、N,⊙O的半径为r,求Rt△CMN的周长.查看答案和解析>>
科目: 来源: 题型:解答题
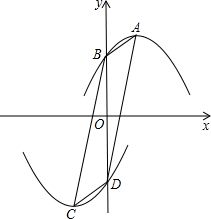 如图,抛物线l1:y=-x2+2bx+c(b>0)的顶点为A,与y轴交于点B;若抛物线l2与l1关于原点O成中心对称,其顶点为C,与y轴交于点D;其中点A、B、C、D中的任意三点都不在同一条直线上.
如图,抛物线l1:y=-x2+2bx+c(b>0)的顶点为A,与y轴交于点B;若抛物线l2与l1关于原点O成中心对称,其顶点为C,与y轴交于点D;其中点A、B、C、D中的任意三点都不在同一条直线上.查看答案和解析>>
科目: 来源: 题型:解答题
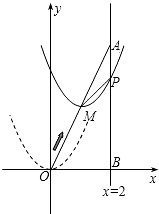 如图,在平面直角坐标系中,已知A点坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知A点坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.查看答案和解析>>
科目: 来源: 题型:解答题
| 数 据 | 平均数 | 方差 |
| x1,x2,…,xn | $\overline{X}$ | S2 |
| x1+a,x2+a,…,xn+a | $\overline{x}$+a | S2 |
| mx1,mx2,…,mxn | m$\overline{x}$ | m2S2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com