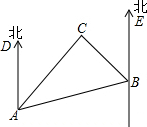13．海面上的A，B，C三艘船的平面图如图所示，C船在A船的北偏东55°方向，B船在A船的北偏东85°方向，C船在B船的北偏西25°方向．
（1）从B船看A，C两船的视角∠ABC是多少度？
（2）从C船看A，B两船的视角∠ACB是多少度？

12．在△ABC中，∠C=90°，∠B=55°点D在边BC上，点E在CN的延长线上，连接DE，∠E=25°，求∠BFD的度数．

11．如图，在△ABC中，∠A=30°，若∠B=∠C，则∠B的度数是75度．

10．如图，将含30°角的三角板的直角顶点放在直尺的一边上，若∠1=40°，则∠2的度数为（　　）

A．

90°

B．

80°

C．

75°

D．

70°

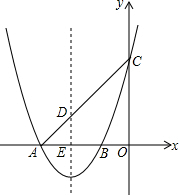9．如图，抛物线y=x²+4x+3交x轴于A、B两点，（A在B左侧），交y轴于点C，
（1）求抛物线的对称轴及点A的坐标；
（2）在平面直角坐标系xOy中是否存在点P，与A、B、C三点构成一个平行四边形？若存在，请写出点P的坐标；若不存在，请说明理由．

8．某公司在成立之初投入了12500元准备销售某种商品，又以每件40元的进价购进了一批这种商品，按规定：该商品每件售价不得低于80元且不得高于150元；
（1）若第1个月最多能销售250件该商品，为了在第1个月内收回投入的资金，每件商品的利润率至少为多少？
（2）在第1个月刚好收回投入的资金的基础上，公司决定在第2个月再追加2000元扩大销售，由于市场原因，该商品的销量出现下滑，经市场调查发现，第二个月该商品的销量y（件）与售价x（元）之间满足关系式：y=-2x+240，为了完成收回投资并盈利1000元的任务，2月份该商品的售价应当定为多少元；
（3）从第3个月开始，销量与售价的关系趋于稳定且满足：y=-x+196，公司决定每销售1件该商品就捐赠a元利润（a≥1）给贫困山区的希望小学，并且当销售价格大于120元时，扣除捐赠后的利润随x的增大而减小．直接写出a的取值范围．

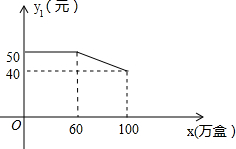7．有一个茶叶厂，该厂的茶叶主要有两种销售方式，一种方式是卖给茶叶经销商，另一种方式是在各超市的柜台进行销售，每年该厂生产的茶叶都可以全部销售，该茶叶厂每年可以生产茶叶100万盒，其中，卖给茶叶经销商每盒茶叶的利润y₁（元）与销售量x（万盒）之间的函数关系如图所示；在各超市柜台销售的每盒利润y₂（元）与销售量x（万盒）之间的函数关系为：y₂=$\left\{\begin{array}{l}{40（0≤x≤60）}\\{\frac{3}{4}x+5（60＜x≤100）}\end{array}\right.$
（1）写出该茶叶厂卖给茶叶经销商的销售总利润z₁（万元）与其销售量x（万盒）之间的函数关系式，并指出x的取值范围；
（2）求出该茶叶厂在各超市柜台销售的总利润z₂（万元）与卖给茶叶经销商的销售量x（万盒）之间的函数关系式，并指出x的取值范围；
（3）求该茶叶厂每年的总利润w（万元）与卖给茶叶经销商的销售量x（万盒）之间的函数关系式，并帮助该茶叶厂确定卖给茶叶经销商和在各超市柜台的销量各为多少万盒时，该公司的年利润最大．

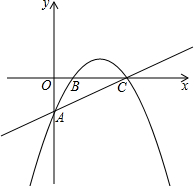6．如图：在平面直角坐标系中，直线$y=\frac{1}{2}x-2$分别交x、y轴于C、A，抛物线y=-$\frac{1}{2}$x²+bx+c经过A、C两点，交x轴于另外一点B．
（1）求抛物线的解析式；
（2）点P为直线AC上方抛物线上的一点，PH⊥AC于H，设点P 的横坐标为t，线段PH的长为d，求出d与t的函数关系式；
（3）在（2）的条件下，当线段d取得最大值时，在对称轴右侧的抛物线上是否存在点R，直线PR交直线AC于Q，使得$\frac{RQ}{PQ}=\frac{3}{4}$？若存在，求出点R的横坐标；若不存在，请说明理由．

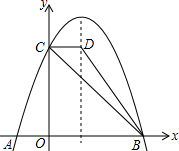5．如图，抛物线y=a（x-1）²+4与x轴交于点A，B，与y轴交于点C，过点C作CD∥x轴交抛物线的对称轴于点D，连接BD，已知点A的坐标为（-1，0）
（1）求该抛物线的解析式；
（2）求梯形COBD的面积．
（3）直线BC上方的抛物线上是否存在一点P，使△PBC的面积最大？若存在，求出点P的坐标；若不存在，请说明理由．

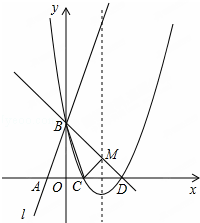4．如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．
（1）求直线BD和抛物线的解析式；
（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标；
（3）在抛物线上是否存在点P，使S_△PBD=6？若存在，求出点P的坐标；若不存在，说明理由；
（4）点Q是抛物线对称轴上一动点，是否存在点Q使得|BQ-CQ|的值最大，若存在，请直接写出点Q的坐标；若不存在，请说明理由．