
科目: 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:解答题
如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,求∠BAD的度数.
AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,求∠BAD的度数.

查看答案和解析>>
科目: 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,直线 与双曲线
与双曲线 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线 的解析式;
的解析式;
(2)若点P在x轴上,且 ,求点P的坐 标(直接写出结果).
,求点P的坐 标(直接写出结果).

查看答案和解析>>
科目: 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:解答题
列方程或方程组解应用题:
在某场CBA比赛中,某位运动员的技术统计如下表所示:
技术 | 上场时间(分钟) | 出手投篮(次) | 投中 (次) | 罚球得分(分) | 篮板 (个) | 助攻(次) | 个人总得分(分) |
数据 | 38 | 27 | 11 | 6 | 3 | 4 | 33 |
注:(1)表中出手投篮次数和投中次数均不包括罚球;
(2)总得分=两分球得分+三分球得分+罚球得分.
根据以上信息,求本场比赛中该运动员投中两分球和三分球各几个.
查看答案和解析>>
科目: 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:解答题
如图,四边形ABCD为平行四边形,∠BAD的角平分线AF交CD于点E,交BC的延长线于点F.
(1)求证:BF=CD;
(2)连接BE,若BE⊥AF,∠BFA=60°,BE= ,求平行四边形ABCD的周长.
,求平行四边形ABCD的周长.

查看答案和解析>>
科目: 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:解答题
阅读下列材料:
“共享单车”是指企业与政府合作,在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车共享的一种服务,是共享经济的一种新形态.共享单车的出现让更多的用户有了更好的代步选择.自行车也代替了一部分公共交通甚至打车的出行.
Quest Mobile监测的M型与O型单车从2016年10月——2017年1月的月度用户使用情况如下表所示:

根据以上材料解答下列问题:
(1)仔细阅读上表,将O型单车总用户数用折线图表示出来,并在图中标明相应数据;
(2)根据图表所提提供的数据,选择你所感兴趣的方面,写出一条你发现的结论.
查看答案和解析>>
科目: 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:解答题
如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB, DF.
(1)求证:DF是⊙O的切线;
(2)若DB平分∠ADC,AB=a,  ∶DE=4∶1,写出求DE长的思路.
∶DE=4∶1,写出求DE长的思路.

查看答案和解析>>
科目: 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:解答题
二次函数 ,其中
,其中 .
.
(1)求该二次函数的对称轴方程;
(2)过动点C(0,  )作直线
)作直线 ⊥y轴.
⊥y轴.
① 当直线 与抛物线只有一个公共点时, 求
与抛物线只有一个公共点时, 求 与
与 的函数关系;
的函数关系;
② 若抛物线与x轴有两个交点,将抛物线在 轴下方的部分沿
轴下方的部分沿 轴翻折,图象的其余部分保持不变,得到一个新的图象. 当
轴翻折,图象的其余部分保持不变,得到一个新的图象. 当 =7时,直线
=7时,直线 与新的图象恰好有三个公共点,求此时
与新的图象恰好有三个公共点,求此时 的值;
的值;
(3)若对于每一个给定的x的值,它所对应的函数值都不小于1,求 的取值范围.
的取值范围.

查看答案和解析>>
科目: 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:解答题
在等腰△ABC中,
(1)如图1,若△ABC为等边三角形,D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,则∠BDE的度数为___________;
(2)若△ABC为等边三角形,点D为线段BC上一动点(不与B,C重合),连接AD并将线段AD绕点D逆时针旋转60°得到线段DE,连接BE.
①根据题意在图2中补全图形;
②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.经过与同学们的充分讨论,形成了几种证明的思路:
思路1:要证明CD=BE,只需要连接AE,并证明△ADC≌△AEB;
思路2:要证明CD=BE,只需要过点D作DF∥AB,交AC于F,证明△ADF≌△DEB;
思路3:要证明CD=BE,只需要延长CB至点G,使得BG=CD,证明△ADC≌△DEG;
……
请参考以上思路,帮助小玉证明CD=BE.(只需要用一种方法证明即可)
(3)小玉的发现启发了小明:如图3,若AB=AC=kBC,AD=kDE,且∠ADE=∠C,此时小明发现BE,BD,AC三者之间满足一定的的数量关系,这个数量关系是______________________.(直接给出结论无须证明)

查看答案和解析>>
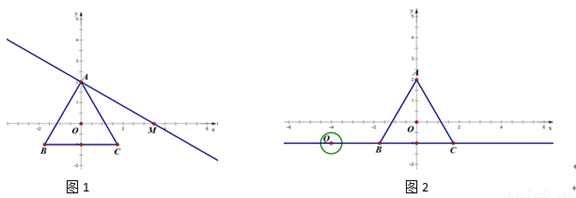
科目: 来源:2017届北京市东城区九年级5月综合练习(一模)数学试卷(解析版) 题型:解答题
设平面内一点到等边三角形中心的距离为d,等边三角形的内切圆半径为r,外接圆半径为R .对于一个点与等边三角形,给出如下定义:满足r≤d≤R的点叫做等边三角形的中心关联点.在平面直角坐标系xOy中,等边△ABC的三个顶点的坐标分别为A(0,2),B(﹣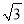 ,﹣1),C(
,﹣1),C(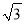 ,﹣1).
,﹣1).
(1)已知点D(2,2),E(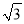 ,1),F(
,1),F(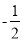 ,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;
,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;
(2)如图1,过点A作直线交x轴正半轴于M,使∠AMO=30°.
①若线段AM上存在等边△ABC的中心关联点P(m,n),求m的取值范围;
②将直线AM向下平移得到直线y=kx+b,当b满足什么条件时,直线y=kx+b上总存在等边△ABC的中心关联点;(直接写出答案,不需过程)
(3)如图2,点Q为直线y=﹣1上一动点,⊙Q的半径为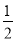 .当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
.当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com