
科目: 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:解答题
一只不透明的袋子中,装有三个分别标记为“-1”、“2”、“ -3”的球,这三个球除了标记不同外,其余均相同.搅匀后,从中摸出一个球,记录球上的标记为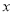 后,放回袋中并搅匀,再从中摸出一个球,再次记录球上的标记为
后,放回袋中并搅匀,再从中摸出一个球,再次记录球上的标记为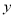 ,最终结果记录为
,最终结果记录为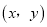 .
.
(1)请用“画树状图”或“列表”等方法写出上述实验中所记录球上标记的所有可能的结果;
(2)若将记录结果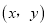 看成平面直角坐标系中的一点,求
看成平面直角坐标系中的一点,求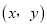 是第二象限内的点的概率.
是第二象限内的点的概率.
查看答案和解析>>
科目: 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:解答题
已知二次函数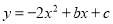 的图像经过点A(0,2)和B(-1,-4).
的图像经过点A(0,2)和B(-1,-4).
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为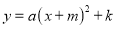 的形式;
的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
(1).(2)C(1,4);1. 【解析】分析:(1)待定系数法求解可得解析式,进一步配方即可得答案; (2)根据顶点式得出C的坐标,由三角形的面积公式可得答案. 本题解析:(1)将点A(0,2)和B(?1,?4)代入y=?2x²+bx+c, 得: 解得: , ∴抛物线的解析式为y=?2x²+4x+2; y=?2x²+4x+2=?2(x²?2x+1?1)+...查看答案和解析>>
科目: 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:解答题
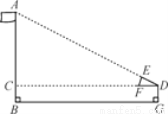
如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行并使直角边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=25米,求旗杆AB的高度.
查看答案和解析>>
科目: 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:解答题
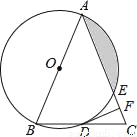
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目: 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:解答题
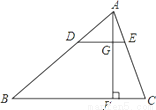
如图,AF是△ABC的高,点D、E分别在AB、AC上,且DE∥BC,DE交AF于点G.设AD=5,AB=15,AC=12,GF=6.
(1)求AE的长;
(2)求点A到DE的距离AG的长.
查看答案和解析>>
科目: 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:解答题
某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进货支出).经过若干年销售得知,年销售量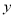 (万件)是销售单价
(万件)是销售单价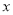 (元)的一次函数,并得到如下部分数据:
(元)的一次函数,并得到如下部分数据:
销售单价 | 12 | 14 | 16 | 18 |
年销售量 | 7 | 6 | 5 | 4 |
(1)求出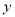 关于
关于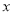 的函数关系式;
的函数关系式;
(2)写出该公司销售这种产品的年利润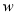 (万元)关于销售单价
(万元)关于销售单价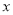 (元)的函数关系式;当销售单价
(元)的函数关系式;当销售单价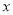 为何值时,年利润最大?
为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于20万元(请直接写出销售单价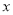 的范围).
的范围).
查看答案和解析>>
科目: 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:解答题
(【材料阅读】阅读下列一段文字,然后回答下列问题.
已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算:
MN=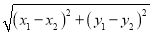 .
.
例如:已知P(3,1)、Q(1,﹣2),则这两点间的距离PQ=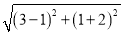 =
=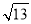 .
.
【直接应用】
(1)已知A(2,-3)、B(-4,5),试求A、B两点间的距离;
(2)已知△ABC的顶点坐标分别为A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.
【深度应用】
(3)如图,在平面直角坐标系xOy中,二次函数y=x2﹣4的图象与x轴相交于两点A、B,(点A在点B的左边)
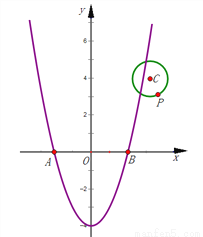
①求点A、B的坐标;
②设点P(m,n)是以点C(3,4)为圆心、1为半径的圆上一动点,求PA2+PB2的最大值;
(1)AB=10; (2)△ABC是直角三角形;(3)①A(-2,0)B(2,0);②80. 【解析】分析:(1)依据两点间的距离公式可求得AB的长;(2)依据两点间的距离公式可求得AB、AC、BC的长,然后依据勾股定理的逆定理可对△ABC的形状作出判断;(3)①令y=0得:x²-4=0,解得x=2或x=-2,故此可得到A,B的坐标;②首先依据两点间的距离公式表示出PA²+PB²的长,通过化...查看答案和解析>>
科目: 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:解答题
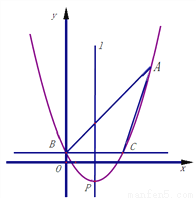
如图1,已知抛物线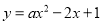 经过点
经过点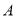 (9,10),交
(9,10),交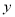 轴于点
轴于点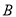 ,直线
,直线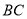 ∥
∥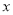 轴,点
轴,点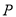 是直线
是直线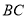 下方抛物线上的动点.
下方抛物线上的动点.
(1)直接写出抛物线的解析式为 ,点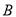 的坐标为 、
的坐标为 、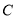 的坐标为 _;
的坐标为 _;
(2)过点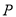 且与
且与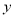 轴平行的直线
轴平行的直线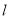 与直线
与直线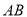 、
、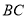 分别交于点
分别交于点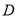 、
、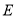 ,当四边形
,当四边形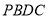 的面积最大时,求
的面积最大时,求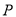 点的坐标;
点的坐标;
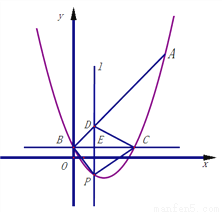
(3)如图2,当点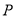 为抛物线的顶点时,在直线
为抛物线的顶点时,在直线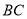 上是否存在点
上是否存在点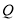 ,使得以
,使得以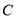 、
、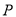 、
、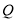 为顶点的三角形与
为顶点的三角形与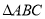 相似,若存在,求出点
相似,若存在,求出点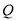 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

查看答案和解析>>
科目: 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:填空题
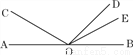
如图,图中的角总共有____________个.
查看答案和解析>>
科目: 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:填空题
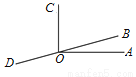
如图,点B、O、D在同一直线上,若∠AOB=17°30′,∠COD=107°29′,则∠AOC= _____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com