练习册

  • 练习册
  • 试题
    相关习题
     0  321274  321282  321288  321292  321298  321300  321304  321310  321312  321318  321324  321328  321330  321334  321340  321342  321348  321352  321354  321358  321360  321364  321366  321368  321369  321370  321372  321373  321374  321376  321378  321382  321384  321388  321390  321394  321400  321402  321408  321412  321414  321418  321424  321430  321432  321438  321442  321444  321450  321454  321460  321468  366461 

    科目： 来源：贵州省2017-2018学年八年级（上）期中数学试卷 题型：填空题

    小明从平面镜中看到镜子对面电子钟示数如图所示，这时的时刻应是 ．

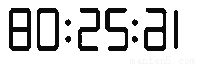
    16∶25∶08 【解析】【解析】 ∵是从镜子中看， ∴对称轴为竖直方向的直线， ∵5的对称数字为2，2的对称数字是5，镜子中数字的顺序与实际数字顺序相反， ∴这时的时刻应是16：25：08．

    查看答案和解析>>

    科目： 来源：贵州省2017-2018学年八年级（上）期中数学试卷 题型：填空题

    如图，Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，CD=4，则点D到AB的距离为 ．

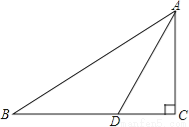
    4． 【解析】试题分析：直接根据角平分线的性质可得出结论．∵Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，CD=4，∴点D到AB的距离为4． 故答案为：4．

    查看答案和解析>>

    科目： 来源：贵州省2017-2018学年八年级（上）期中数学试卷 题型：填空题

    一个正多边形的每一个外角都是36°，则这个正多边形的边数是 ．

    10 【解析】试题分析：根据正多边形的性质，边数等于360°除以每一个外角的度数． 【解析】 ∵一个多边形的每个外角都是36°， ∴n=360°÷36°=10， 故答案为：10．

    查看答案和解析>>

    科目： 来源：贵州省2017-2018学年八年级（上）期中数学试卷 题型：填空题

    图示，点B在AE上，∠CBE=∠DBE，要使△ABC≌△ABD，还需添加一个条件是__（填上适当的一个条件即可）

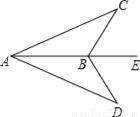
    BC=BD(答案不唯一) 【解析】试题分析：根据∠CBE=∠DBE可得∠ABC=∠ABD，如果利用SAS来判定可以添加BC=BD，如果利用ASA来判定可以添加∠CAB=∠DAB，如果利用AAS来判定可以添加∠C=∠D.

    查看答案和解析>>

    科目： 来源：贵州省2017-2018学年八年级（上）期中数学试卷 题型：填空题

    如果等腰三角形一腰上的高和与另一腰的夹角为30°，则它的顶角度数为 ．

    60度或120度 【解析】 试题分析：由于已知条件没有明确这条在三角形内部还有外部两种情况进行分析． 当高在内部时，顶角= ； 当高在外部时，得到顶角的外角=； 当顶角=． 故答案为：或．

    查看答案和解析>>

    科目： 来源：贵州省2017-2018学年八年级（上）期中数学试卷 题型：填空题

    如图2，在等腰直角△ABC中，∠C＝90°，AC＝BC，AD平分∠BAC交BC于D，DE⊥AB于D，若AB＝10，则△BDE的周长等于 .

    10 【解析】∵AD平分∠CAB，AC⊥BC于点C，DE⊥AB于E，∴CD=DE． 又∵AD=AD，∴Rt△ACD≌Rt△AED，∴AC=AE． 又∵AC=BC，∴AC=AE， ∴△DBE的周长为DE+BD+EB=CD+BD+EB=BC+EB=AC+EB=AE+EB=AB=10

    查看答案和解析>>

    科目： 来源：贵州省2017-2018学年八年级（上）期中数学试卷 题型：填空题

    如图，在Rt△ABC中，∠C=90°，DE是AB的垂直平分线，且∠BAD：∠BAC=1：3，则∠B=_____．

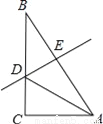
    22.5° 【解析】∵∠BAD：∠BAC=1：3， 设∠BAD=x°，则∠BAC=3x°， ∵DE是AB的垂直平分线， ∴AD=BD， ∴∠DAB=∠B=x°， ∵∠C=90°， ∴∠BAC+∠B=90°， ∴3x+x=90， 解得：x=22.5， ∴∠B=22.5°， 故答案为：22.5°．

    查看答案和解析>>

    科目： 来源：贵州省2017-2018学年八年级（上）期中数学试卷 题型：解答题

    要在燃气管道L上修建一个泵站P，分别向A，B两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短？在图上画出P点位置，不写作法，保留痕迹．

    见解析 【解析】试题分析：作出A镇关于燃气管道的对称点A′，连接A′B，根据轴对称确定最短路线问题，A′B与燃气管道的交点即为所求的点P的位置． 试题解析：作点A关于燃气管道L的对称点A′，连接A′B交L于点P，即点P即为所求．

    查看答案和解析>>

    科目： 来源：贵州省2017-2018学年八年级（上）期中数学试卷 题型：解答题

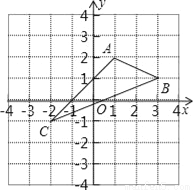
    如图，在平面直角坐标系中，A（1，2），B（3，1）C（﹣2，﹣1）．

    （1）在图中作出△ABC关于y轴对称的△A1B1C1，并写出对称点的坐标；

    （2）求△ABC的面积．

    （1）A1（﹣1，2）、B1（﹣3，1）、C1（2，﹣1）；（2）4.5. 【解析】试题分析：（1）分别作出三角形三顶点关于y轴的对称点，再顺次连接可得； （2）利用割补法求解可得． 试题解析：（1）如图所示，△A1B1C1即为所求； A1（﹣1，2）、B1（﹣3，1）、C1（2，﹣1）； （2）S△ABC=5×3﹣×1×2﹣×2×5﹣×3×3=4.5．

    查看答案和解析>>

    科目： 来源：贵州省2017-2018学年八年级（上）期中数学试卷 题型：解答题

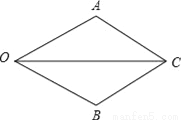
    如图，OA=OB，AC=BC．求证：∠AOC=∠BOC．

    证明见解析 【解析】试题分析：根据SSS推出△OAC≌△OBC，根据全等三角形的性质定理推出即可． 试题解析：在△OAC和△OBC中， ， ∴△OAC≌△OBC（SSS）， ∴∠AOC=∠BOC．

    查看答案和解析>>

    同步练习册答案