
科目: 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
一个正方形的侧面展开图有( )个全等的正方形.
A. 2个 B. 3个 C. 4个 D. 6个
C 【解析】试题分析:根据正方体的特征即可判断. 一个正方体的侧面展开图有4个全等的正方形, 故选C.查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
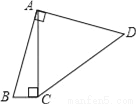
如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
A. y=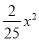 B. y=
B. y=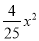 C. y=
C. y=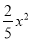 D. y=
D. y=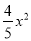
查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
下列命题中,是真命题的是( )
①面积相等的两个直角三角形全等;
②对角线互相垂直的四边形是正方形;
③将抛物线 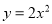 向左平移4个单位,再向上平移1个单位可得到抛物线
向左平移4个单位,再向上平移1个单位可得到抛物线 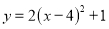 ;
;
④两圆的半径R、r分别是方程x2-3x+2=0 的两根,且圆心距d=3, 则两圆外切.
A. ① B. ② C. ③ D. ④
D 【解析】试题解析:①面积相等的两个直角三角形不一定全等,原命题是假命题; ②对角线互相垂直的四边形不一定是正方形,原命题是假命题; ③将抛物线y=2x2向左平移4个单位,再向上平移1个单位可得到抛物线y=2(x+4)2+1,原命题是假命题; ④两圆的半径R、r分别是方程x2-3x+2=0的两根,且圆心距d=3,则两圆外切,是真命题; 故选D.查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
下列命题,其中真命题是( )
A. 方程x2=x的解是x=1
B. 6的平方根是±3
C. 有两边和一个角分别对应相等的两个三角形全等
D. 连接任意四边形各边中点的四边形是平行四边形
D 【解析】试题分析:方程的解为, ,故不正确;3的平方根为±,故不正确;有两边对应相等,且夹角相等的两三角形全等,故不正确;根据三角形中位线的性质可知连接任意四边形各边中点的四边形是平行四边形,故正确. 故选D查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
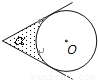
A. 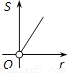 B.
B. 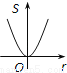 C.
C. 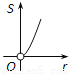 D.
D. 
查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
如图所示,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论: ①AD⊥BC;②∠EDA=∠B;③OA= 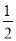 AC;④DE是⊙O的切线, 正确的有()
AC;④DE是⊙O的切线, 正确的有()
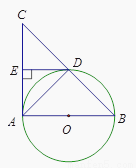
A. 1个 B. 2个 C. 3个 D. 4个
D 【解析】【解析】 ∵AB是直径, ∴∠ADB=90°, ∴AD⊥BC,故①正确; ∵点D是BC的中点, ∴CD=BD, ∴△ACD≌△ABD(SAS), ∴AC=AB,∠C=∠B, ∵OD=OB, ∴∠B=∠ODB, ∴∠ODB=∠C,OD∥AC, ∴∠ODE=∠CED, ∴ED是圆O的切线,故④正确; 由弦切角定...查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
下列几何体的主视图既是中心对称图形又是轴对称图形的是( )
A. 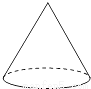 B.
B. 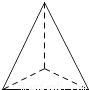 C.
C. 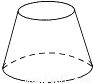 D.
D. 
查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
已知抛物线y=k(x+1)(x-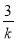 )与x轴交于点A、B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线有( )
)与x轴交于点A、B,与y轴交于点C,则能使△ABC为等腰三角形的抛物线有( )
A. 5条 B. 4条 C. 3条 D. 2条
B 【解析】试题分析:整理抛物线解析式,确定出抛物线与x轴的一个交点A和y轴的交点C,然后求出AC的长度,再分①k>0时,点B在x轴正半轴时,分AC=BC、AC=AB、AB=BC三种情况求解;②k<0时,点B在x轴的负半轴时,点B只能在点A的左边,只有AC=AB一种情况列式计算即可.查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是
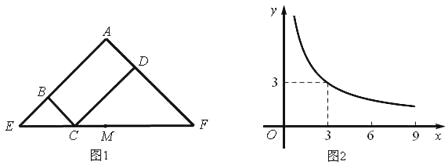
A. 当x=3时,EC<EM B. 当y=9时,EC>EM
C. 当x增大时,EC·CF的值增大。 D. 当y增大时,BE·DF的值不变。
B 【解析】试题分析:由图象可知,反比例函数图象经过(3,3),应用待定系数法可得该反比例函数关系式为,因此, 当x=3时,y=3,点C与点M重合,即EC=EM,选项A错误; 根据等腰直角三角形的性质,当x=3时,y=3,点C与点M重合时,EM=, 当y=9时, ,即EC=,所以,EC<EM,选项B错误; 根据等腰直角三角形的性质,EC= ,CF= , 即EC·CF=,为定...查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型:单选题
在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
A. 16个 B. 15个 C. 13个 D. 12个
D 【解析】试题分析:由摸到红球的频率稳定在25%附近得出口袋中得到红色球的概率,进而求出白球个数即可. 【解析】 设白球个数为:x个, ∵摸到红色球的频率稳定在25%左右, ∴口袋中得到红色球的概率为25%, ∴=, 解得:x=12, 故白球的个数为12个. 故选:D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com