
科目: 来源:山东省滨州市惠民县2018届九年级上学期期末数学试卷 题型:解答题
(1)用配方法解方程: 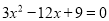 .
.
(2)用公式法解方程: 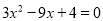 .
.
查看答案和解析>>
科目: 来源:山东省滨州市惠民县2018届九年级上学期期末数学试卷 题型:解答题
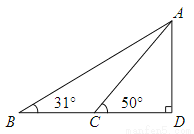
据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
查看答案和解析>>
科目: 来源:山东省滨州市惠民县2018届九年级上学期期末数学试卷 题型:解答题
已知二次函数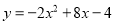 ,完成下列各题:
,完成下列各题:
(1)将函数关系式用配方法化为 y=a(x+h)2+k形式,并写出它的顶点坐标、对称轴.
(2)若它的图象与x轴交于A、B两点,顶点为C,求△ABC的面积.
(1) 抛物线的顶点坐标为(2,4),对称轴为直线x=2.(2) . 【解析】试题分析: (1)用“配方法”把二次函数化为顶点式:y=a(x+h)2+k的形式即可得到本题答案; (2)由(1)中结果可得点C的坐标,解方程可求得A、B的坐标,由此即可求出△ABC的面积. 试题解析: (1)∵y=-2x2+8x-4 =-2(x2-4x)-4 =-2(x2-4x...查看答案和解析>>
科目: 来源:山东省滨州市惠民县2018届九年级上学期期末数学试卷 题型:解答题
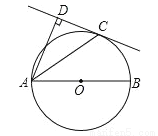
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为3,AD=4,求CD的长.
查看答案和解析>>
科目: 来源:山东省滨州市惠民县2018届九年级上学期期末数学试卷 题型:解答题
如图,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线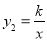 (x<0)分别交于点C(-1,2)、D(a,1).
(x<0)分别交于点C(-1,2)、D(a,1).
(1)分别求出直线及双曲线的解析式;
(2)利用图象直接写出,当x在什么范围内取值时,y1>y2.
(3)请把直线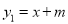 上y1<y2时的部分用黑色笔描粗一些.
上y1<y2时的部分用黑色笔描粗一些.
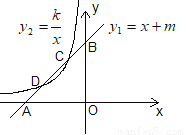
查看答案和解析>>
科目: 来源:山东省滨州市惠民县2018届九年级上学期期末数学试卷 题型:解答题
某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元.如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
第二个月的单价应是70元. 【解析】试题分析: 设第二个月降价元,则由题意可得第二个月的销售单价为元,销售量为件,由此可得第二个月的销售额为元,结合第一个月的销售额为元和第三个月的销售额为元及总的利润为9000元,即可列出方程,解方程即可求得第二个月的销售单价. 试题解析: 设第二个月的降价应是元,根据题意,得: 80×200+(80-x)(200+10x)+40[8...查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测九年级数学试卷 题型:单选题
Rt△ABC中,∠C=90°,a=4,b=3,则cosA的值是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测九年级数学试卷 题型:单选题
有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是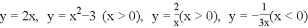 ,将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是
,将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是
A.  B.
B.  C.
C.  D. 1
D. 1
查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测九年级数学试卷 题型:单选题
某几何体的三视图如图,则该几何体是( )

A. 圆柱 B. 圆锥 C. 球 D. 长方体
B 【解析】试题解析:从主视图和左视图可以看出这个几何体是椎体,从俯视图可以看出这个几何体不是棱锥,是圆锥, 故选A.查看答案和解析>>
科目: 来源:广西合浦县2017年秋季学期教学质量监测九年级数学试卷 题型:单选题
如图所示几何体的左视图是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com