
科目: 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:单选题
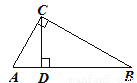
如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于sinA的是( )
A. 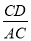 B.
B. 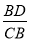 C.
C. 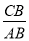 D.
D. 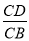
查看答案和解析>>
科目: 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:单选题
在平面直角坐标系中,△ABC顶点A的坐标为(2,3).若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比为 ,则点A′的坐标为( )
,则点A′的坐标为( )
A. (3,  ) B. (3,
) B. (3,  )或(-3,
)或(-3,  )
)
C. ( ,-2) D. (
,-2) D. ( ,2)或(
,2)或( ,-2)
,-2)
查看答案和解析>>
科目: 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:单选题
如图,矩形OABC的面积为24,它的对角线OB与双曲线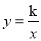 相交于点D,且D为OB的中点,则k的值为( )
相交于点D,且D为OB的中点,则k的值为( )
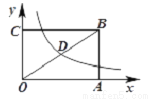
A. 3 B. 6 C. 9 D. 12
B 【解析】根据反比例函数解析式可得D点的坐标为(),然后根据中点的性质,可得B点的坐标为:(),然后可根据矩形的面积可求得2x×=24,解得k=6. 故选:B.查看答案和解析>>
科目: 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:填空题
已知tanA=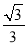 ,则锐角A的度数是__________.
,则锐角A的度数是__________.
查看答案和解析>>
科目: 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:填空题
中午12点,身高为165cm的小冰直立时影长55cm,同学小雪此时在同一地点直立时影长为57cm,那么小雪的身高为__________cm.
171查看答案和解析>>
科目: 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:填空题
二次函数y=(x-2m)2+1,当m<x<m+1时,y随x的增大而减小,则m的取值范围是__________.
m>1 【解析】由条件可知二次函数对称轴为x=2m,且开口向上,由二次函数的性质可知在对称轴的左侧时y随x的增大而减小,可求得m+1<2m,即m>1. 故答案为:m>1.查看答案和解析>>
科目: 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的正弦值是__________.

查看答案和解析>>
科目: 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:填空题
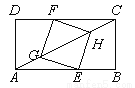
如图,在矩形ABCD中,AB=4,BC=2.点E在边AB上,点F在边CD上,点G,H在对角线AC上.若四边形EGFH是菱形,则AE的长是__________.
查看答案和解析>>
科目: 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:填空题
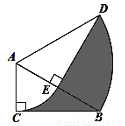
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,BC=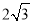 ,将△ABC绕点A逆时针旋转60°后得到△ADE,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是__________(结果保留π).
,将△ABC绕点A逆时针旋转60°后得到△ADE,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是__________(结果保留π).
查看答案和解析>>
科目: 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:解答题
在△ABC中,∠C=90°,AB=13,BC=5,求∠A的正弦值、余弦值和正切值.
. 【解析】试题分析:根据解直角三角形的意义,根据勾股定理求出AC的长,然后根据正弦、余弦、正切的概念可求解. 试题解析:∵∠C=90°,AB=13,BC=5, ∴. ∴, , .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com