
科目: 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
观察下列各式的规律:
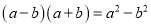
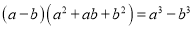
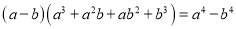
……
可得到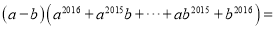 _______.
_______.
查看答案和解析>>
科目: 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
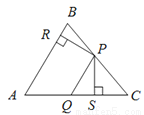
如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS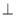 AC,PR
AC,PR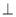 AB,若AQ
AB,若AQ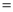 PQ,PR
PQ,PR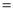 PS,则下列结论:①AS
PS,则下列结论:①AS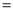 AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ=
AR;②QP∥AR;③△BRP ≌△CPS;④S四边形ARPQ=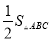 .其中正确的结论有____________(填序号).
.其中正确的结论有____________(填序号).
查看答案和解析>>
科目: 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
分解因式:① -a4+16;②6xy2-9x2y-y3
(1)(2-a)(2+a)(4+a2);(2)-y2(y-3x)2. 【解析】分析:(1)利用平方差公式分解即可;(2)先提公因式,再利用完全平方公式分解即可. 本题解析: (1) (2)查看答案和解析>>
科目: 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
已知4x=3y,求代数式(x-2y)2-(x-y)(x+y)-2y2的值.
原式=3y2-4xy=0 【解析】试题分析:首先利用平方差公式和完全平方公式计算,进一步合并,最后代入求得答案即可. 试题解析:(x-2y)2-(x-y)(x+y)-2y2 =x2-4xy+4y2-(x2-y2)-2y2 =-4xy+3y2 =-y(4x-3y). ∵4x=3y, ∴原式=0.查看答案和解析>>
科目: 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
AD,AE分别是△ABC的高和角平分线.
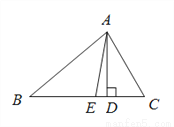
(1)已知∠B=30°,∠C=60°,求∠DAE的度数;
(2)设∠B= x,∠C= y(x < y),请直接写出∠DAE的度数 .(用含x ,y的代数式表示)
(1)∠EAD=15°;(2) ∠EAD= (y-x) 【解析】分析:分析:(1)根据三角形内角和定理求出∠BAC,再根据角平分线的定义求出∠EAC,根据直角三角形两锐角互余求出∠DAC,然后求解即可.(2)同(1)即可得出结果. 本题解析: (1) 由 ∴ 又AE平分, ∴ ∴ (2)查看答案和解析>>
科目: 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
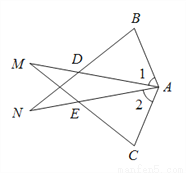
ABN和△ACM的位置如图所示,AB=AC,AD=AE,∠1=∠2.
求证:(1)BD=CE;(2)∠M=∠N.
查看答案和解析>>
科目: 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
化简: 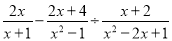 ,然后在不等式
,然后在不等式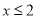 的非负整数解中选择一个适当的数代入求值.
的非负整数解中选择一个适当的数代入求值.
查看答案和解析>>
科目: 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
某超市用5 000元资金购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨了11 000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍.
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?
(1)试销时该品种苹果的进价是5元/千克;(2)超市在两次苹果销售中盈利4160元 【解析】试题分析:(1)设试销时苹果的进货价是x元/斤,根据“11000元购进该种苹果的进货价比试销时多了0.5元,购进苹果数量是试销时的两倍”即可列方程求解; (2)先分别求得两次进的苹果的质量,再分别求得两次销售的利润,从而可以求得结果. (1)设试销时苹果的进货价是x元/斤,由题意得 ...查看答案和解析>>
科目: 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
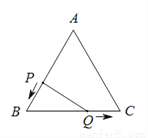
如图,已知△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),则(1)BP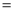 cm,BQ
cm,BQ cm.(用含t的代数式表示)
cm.(用含t的代数式表示)
(2)当t为何值时,△PBQ是直角三角形?
查看答案和解析>>
科目: 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
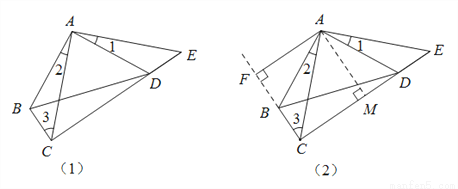
如图(1),在四边形ABCD中,已知∠ABC ∠ADC
∠ADC 180°,AB
180°,AB AD,AB
AD,AB AD,点E在CD的延长线上,∠1
AD,点E在CD的延长线上,∠1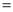 ∠2.
∠2.
(1)求证:∠3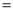 ∠E;
∠E;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的边BC上的高,求证:CE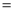 2AF.
2AF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com