
科目: 来源:浙江省台州市2018届九年级下学期第一次月考数学试卷 题型:填空题
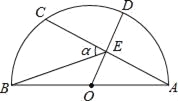
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则sinα的值为 .
查看答案和解析>>
科目: 来源:浙江省台州市2018届九年级下学期第一次月考数学试卷 题型:解答题
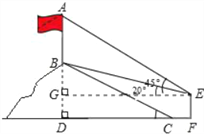
如图山坡上有一根旗杆AB,旗杆底部B点到山脚C点的距离BC为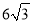 米,斜坡BC的坡度i=1:
米,斜坡BC的坡度i=1: 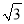 .小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
.小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
(1)求坡角∠BCD;
(2)求旗杆AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
科目: 来源:浙江省台州市2018届九年级下学期第一次月考数学试卷 题型:解答题
阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表8.
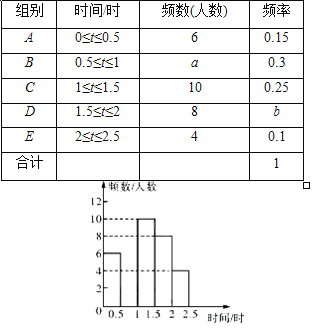
请根据图表中的信息,解答下列问题:
(1)表中的a=______,b=______,中位数落在________组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出2人向全校同学作读书心得报告,请用画树状图或列表法求抽取的2名学生刚好是1名男生和1名女生的概率.
查看答案和解析>>
科目: 来源:浙江省台州市2018届九年级下学期第一次月考数学试卷 题型:解答题
如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.
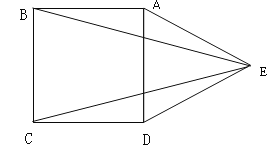
(1)求证:BE=CE.
(2)求∠BEC的度数
查看答案和解析>>
科目: 来源:浙江省台州市2018届九年级下学期第一次月考数学试卷 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
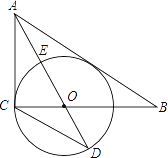
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=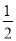 ,求
,求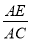 的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
查看答案和解析>>
科目: 来源:浙江省台州市2018届九年级下学期第一次月考数学试卷 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.

(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=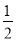 ,求
,求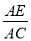 的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
【答案】(1)证明见解析(2)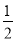 (3)
(3)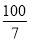
【解析】试题分析:(1)过O作OF⊥AB于F,由角平分线上的点到角两边的距离相等即可得证;(2)连接CE,证明△ACE∽△ADC可得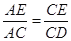 = tanD=
= tanD=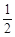 ;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得
;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得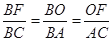 ,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
试题解析:(1)证明:作OF⊥AB于F
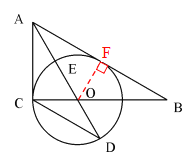
∵AO是∠BAC的角平分线,∠ACB=90º
∴OC=OF
∴AB是⊙O的切线
(2)连接CE
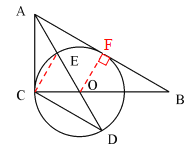
∵AO是∠BAC的角平分线,
∴∠CAE=∠CAD
∵∠ACE所对的弧与∠CDE所对的弧是同弧
∴∠ACE=∠CDE
∴△ACE∽△ADC
∴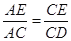 = tanD=
= tanD=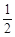
(3)先在△ACO中,设AE=x,
由勾股定理得
(x+3)²="(2x)" ²+3² ,解得x="2,"
∵∠BFO=90°=∠ACO
易证Rt△B0F∽Rt△BAC
得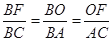 ,
,
设BO=y BF=z
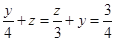
即4z=9+3y,4y=12+3z
解得z=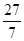 y=
y=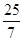
∴AB=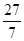 +4=
+4=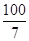
考点:圆的综合题.
【题型】解答题
【结束】
22
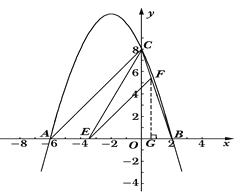
已知:二次函数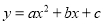 的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
的图象与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且A点坐标为(-6,0).
(1)求此二次函数的表达式;
(2)若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com