
科目: 来源:山东省烟台市2018年中考数学试卷 题型:填空题
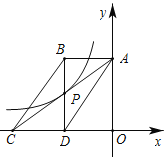
如图,反比例函数y= 的图象经过?ABCD对角线的交点P,已知点A,C,D在坐标轴上,BD⊥DC,?ABCD的面积为6,则k=_____.
的图象经过?ABCD对角线的交点P,已知点A,C,D在坐标轴上,BD⊥DC,?ABCD的面积为6,则k=_____.
查看答案和解析>>
科目: 来源:山东省烟台市2018年中考数学试卷 题型:填空题
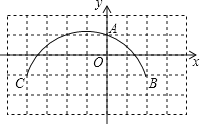
如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为_____.
查看答案和解析>>
科目: 来源:山东省烟台市2018年中考数学试卷 题型:填空题
已知关于x的一元二次方程x2﹣4x+m﹣1=0的实数根x1,x2,满足3x1x2﹣x1﹣x2>2,则m的取值范围是_____.
查看答案和解析>>
科目: 来源:山东省烟台市2018年中考数学试卷 题型:填空题
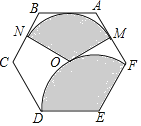
如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
查看答案和解析>>
科目: 来源:山东省烟台市2018年中考数学试卷 题型:解答题
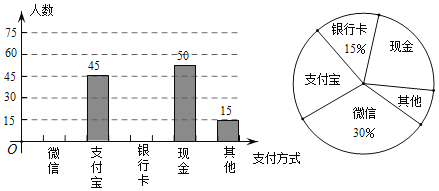
随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.
查看答案和解析>>
科目: 来源:山东省烟台市2018年中考数学试卷 题型:解答题
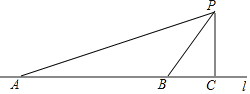
汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速如图,学校附近有一条笔直的公路l,其间设有区间测速,所有车辆限速40千米/小时数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=30米,∠APC=71°,∠BPC=35°.上午9时测得一汽车从点A到点B用时6秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
查看答案和解析>>
科目: 来源:山东省烟台市2018年中考数学试卷 题型:解答题
为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
科目: 来源:山东省烟台市2018年中考数学试卷 题型:解答题
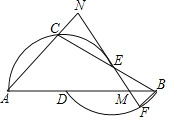
如图,已知D,E分别为△ABC的边AB,BC上两点,点A,C,E在⊙D上,点B,D在⊙E上.F为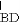 上一点,连接FE并延长交AC的延长线于点N,交AB于点M.
上一点,连接FE并延长交AC的延长线于点N,交AB于点M.
(1)若∠EBD为α,请将∠CAD用含α的代数式表示;
(2)若EM=MB,请说明当∠CAD为多少度时,直线EF为⊙D的切线;
(3)在(2)的条件下,若AD=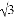 ,求
,求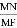 的值.
的值.
查看答案和解析>>
科目: 来源:山东省烟台市2018年中考数学试卷 题型:解答题
(问题解决)
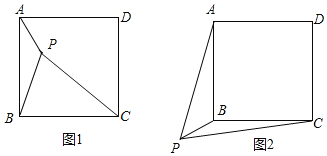
一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.
(类比探究)
如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=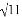 ,求∠APB的度数.
,求∠APB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com