
科目: 来源:北京市2017-2018学年第二学期数学期中试卷 题型:解答题
在《九章算术》中有求三角形面积公式“底乘高的一半”,但是在实际丈量土地面积时,量出高并非易事,所以古人想到了能否利用三角形的三条边长来求面积.我国南宋著名的数学家秦九韶(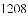
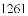
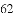
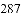
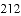
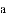
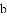
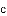
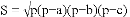 (公式里的
(公式里的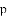
请利用海伦一秦九韶公式解决以下问题:
(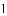
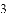
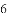
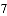
(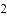
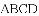
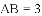
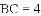
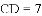
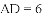
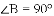
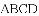
(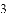
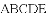
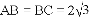 ,
,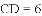
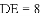
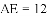
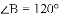
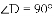
查看答案和解析>>
科目: 来源:北京市2017-2018学年第二学期数学期中试卷 题型:解答题
已知:△ABC是一张等腰直角三角形纸板,∠B=90°,AB=BC=1.
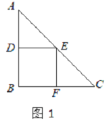
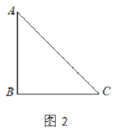
(1)要在这张纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.
(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为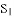 ,则
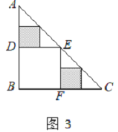
,则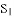 =___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为
=___________;在余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和记为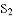 ,则
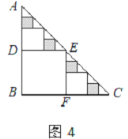
,则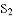 =___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为
=___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和记为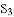 ;按照同样的方法继续操作下去……,第
;按照同样的方法继续操作下去……,第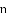
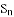 =______________.
=______________.
查看答案和解析>>
科目: 来源:湖南省2018届九年级中考数学模拟试卷 题型:单选题
为了了解内江市2018年中考数学学科各分数段成绩分布情况,从中抽取400名考生的中考数学成绩进行统计分析,在这个问题中,样本是指( )
A. 400
B. 被抽取的400名考生
C. 被抽取的400名考生的中考数学成绩
D. 内江市2018年中考数学成绩
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com