
科目: 来源:四川成都市成华区2017-2018学年度下七年级期中学业水平阶段监测数学试卷 题型:填空题
下图是我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”
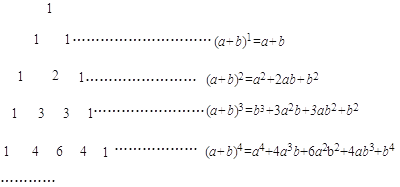
这个三角形给出了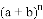
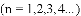
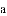
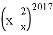 展开式中含有
展开式中含有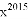 项的系数是__________.
项的系数是__________.
查看答案和解析>>
科目: 来源:四川成都市成华区2017-2018学年度下七年级期中学业水平阶段监测数学试卷 题型:解答题
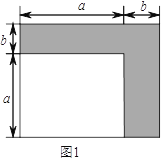
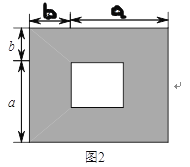
数学课上,我们知道可以用图形的面积来解释一些代数恒等式,如图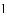
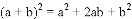 .
.
(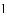
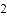
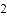
方法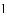
方法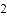
(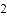
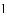
(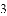
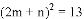 ,
,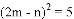 ,请利用(
,请利用(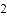

查看答案和解析>>
科目: 来源:四川成都市成华区2017-2018学年度下七年级期中学业水平阶段监测数学试卷 题型:解答题
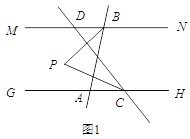
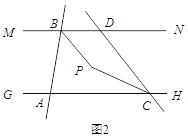
已知:如图所示,直线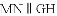
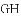
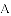
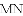
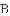
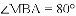
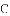
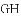
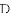
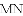
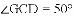
(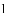
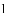
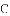
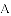
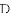
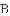
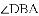
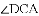
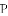
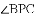
(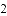
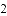
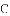
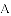
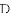
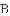
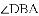
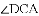
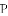
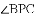
(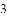
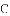
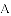
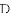
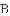
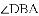
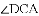
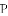
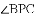
查看答案和解析>>
科目: 来源:四川成都市成华区2017-2018学年度下七年级期中学业水平阶段监测数学试卷 题型:解答题
阅读理解并完成下面问题:
我们知道,任意一个正整数






 (其中
(其中




 ,所以
,所以

 .
.
(




 的值;
的值;
(



(

 的最小值.
的最小值.
查看答案和解析>>
科目: 来源:2017-2018学年数学人教版七年级下册9.1不等式同步练习 题型:单选题
在数学表达式:①-3<0,②3x+5>0,③x2-6,④x=-2,⑤y≠0,⑥x+2≥x中,不等式的个数是( ).
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com