先化简，再求值：，其中

同学们都知道,|5－(－2)|表示5与－2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对的两点之间的距离.试探索：

(1)求|5－(－2)|=___________．

(2)数轴上表示x和-1的两点之间的距离表示为___________．

(3)找出所有符合条件的整数x，使|x+5|+|x-2|=7,这样的整数有___________个．

(4)若x表示一个有理数，且|x-2|+|x+4|＞6，则有理数x的取值范围是_________．

先阅读材料，再回答问题：分解因式：(a-b)2-2(a-b)+1.

【解析】
将“a-b”看成整体，令a-b=M，则原式=M2-2M+1=(M-1)2,再将a-b=M还原，得到：原式=(a-b-1)2.上述解题中用到的是“整体思想”，它是数学中常用的一种思想，请你用整体思想解决下列问题：

（1）分解因式：9+6(x+y)+(x+y)2=____________________.

（2）分解因式：x2-2xy+y2-1=____________________.

（3）若n为正整数，则(n+1)(n+4)(n2+5n)+4的值为某一个整数的平方，试说明理由．

在学习《实数》内容时，我们通过“逐步逼近”的方法可以计算出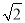的近似值，得出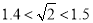.利用“逐步逼近”法，请回答下列问题：

（1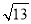）介于连续的两个整数a和b之间，且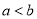，那么a= ，b= ；

（2）若x是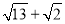的小数部分，y是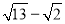的整数部分，求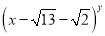的平方根.

如图，是某兴趣小组制作的一图案，长方形长是a，宽是b.图中半圆大小一样.

（1）用含a,b的代数式表示阴影部分的面积；

（2）当a=12，b=5时，求阴影部分的面积．

滴滴快车”是一种便捷的出行工具，计价规则如下表：

随着互联网的不断发展，更多的人们选择了“滴滴快车”出行。假设“滴滴快车”的平均行车速度为50 km/h，请回答下列问题：

（1）小明和小冰各自乘坐“滴滴快车”，行车里程分别为3千米和10千米，请问他们各自需付车费多少钱？

（2）张老师与王老师的家和学校在同一条直线上，位置如图所示。一天，张老师和王老师各自从学校“滴滴快车”回家，分别付车费9.6元和24元。请问，张老师和王老师的家相距多少千米？

湖州市在2017年被评为“全国文明城市”，在评选过程中，湖州市环卫处每天需负责市区范围420千米城市道路的清扫工作，现有环卫工人直接清扫和道路清扫车两种马路清扫方式.已知20名环卫工人和1辆道路清扫车每小时可以清扫20千米马路，30名环卫工人和3辆道路清扫车每小时可以清扫42千米的马路.

（1）1名环卫工人和1辆道路清扫车每小时各能清扫多长的马路？

（2）已知2017年环卫处安排了50名环卫工人参与了直接清扫工作，为保证顺利完成每日的420千米清扫工作，需派出多少辆道路清扫车参与工作（已知2017年环卫工人与清扫车每天工作时间为6小时）？

（3）为了巩固文明城市创建成果，从2018年5月开始，环卫处新增了一辆清扫车参与工作，同时又增加了若干个环卫工人参与直接清扫，使得每日能够较早的完成清扫工作。2018年6月市环卫处扩大清扫范围60千米，同时又增加了20名环卫工人直接参与清扫，此时环卫工人和清扫车每日工作时间仍与5月份相同，那么2018年5月环卫处增加了多少名环卫工人参与直接清扫？

如图1，已知数轴上两点A、B对应的数分别为﹣2、5，点P为数轴上的一动点，其对应的数为x．

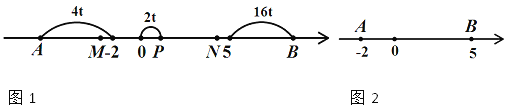
（1）PA= ；PB= （用含x的式子表示）

（2）在数轴上是否存在点P，使PA+PB=10？若存在，请直接写出x的值；若不存在，请说明理由．

（3）如图2，点P以2个单位/s的速度从点O向右运动，同时点A以4个单位/s的速度向左运动，点B以16个单位/s的速度向右运动，在运动过程中，M、N分别是AP、OB的中点，问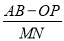： 的值是否发生变化？请说明理由．

如图，AB∥CD，定点E，F分别在直线AB，CD上，在平行线AB、CD之间有一动点P，满足0°<∠EPF<180°.

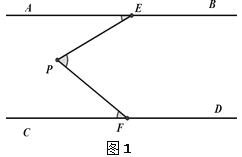
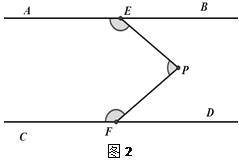
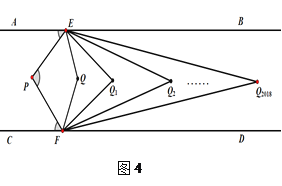
（1）试问∠AEP，∠EPF，∠PFC满足怎样的数量关系？

【解析】
由于点P是平行线AB、CD之间有一动点，因此需要对点P的位置进行分类讨论；如图1，当P点在EF的左侧时，∠AEP，∠EPF，∠PFC满足数量关系为______________，如图2，当P点在EF的右侧时，∠AEP，∠EPF，∠PFC满足数量关系为______________。

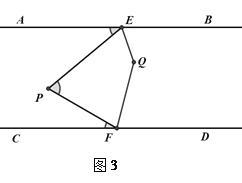
（2）如图3，QE，QF分别平分∠PEB和∠PFD，且点P在EF左侧.

①若∠EPF=60°，则∠EQF=_______°.

②猜想∠EPF与∠EQF的数量关系，并说明理由.

③如图4，若∠BEQ与∠DFQ的角平分线交于点Q1，∠BEQ1与∠DFQ1的角平分线交于点Q2，∠BEQ2与∠DFQ2的角平分线交于点Q3，此次类推，则∠EPF与∠EQ2018F满足怎样的数量关系？（直接写出结果）

下列四个标志中，是轴对称图形的是( )

A. B. C. D.