
科目: 来源:2018-2019学年度第一学期人教版九年级数学_223_实际问题与二次函数_课时同步检测 题型:解答题
定义感知:我们把顶点关于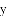
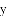
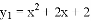 与
与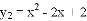 是一对“孪生抛物线”,其“共点”为点
是一对“孪生抛物线”,其“共点”为点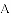
初步运用:
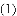
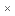
①“孪生抛物线”的“共点”不能分布在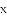
②“孪生抛物线”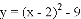 与
与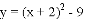 的“共点”坐标为
的“共点”坐标为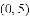
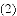
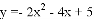 的“孪生抛物线”的解析式为________.
的“孪生抛物线”的解析式为________.
延伸拓展:在平面直角坐标系中,记“孪生抛物线”的两顶点分别为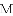
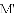
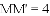
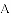
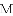
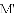
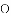
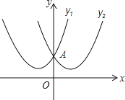
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期人教版九年级数学_223_实际问题与二次函数_课时同步检测 题型:填空题
某果园有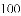
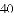
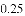
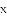
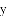
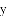
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期人教版九年级数学_223_实际问题与二次函数_课时同步检测 题型:填空题
某果园有100棵橘子树,平均每一棵树结600个橘子.根据经验估计,每多种一颗树,平均每棵树就会少结5个橘子.设果园增种x棵橘子树,果园橘子总个数为y个,则果园里增种 棵橘子树,橘子总个数最多.
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期人教版九年级数学_223_实际问题与二次函数_课时同步检测 题型:解答题
某企业设计了一款工艺品,每件的成本是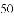
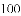
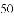
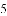
(1)求每天的销售利润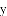
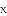
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期人教版九年级数学_223_实际问题与二次函数_课时同步检测 题型:解答题
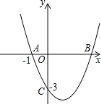
如图,抛物线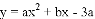 经过
经过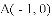
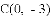
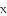
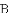
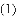
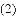
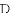
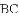
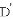 的坐标.
的坐标.
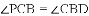
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期人教版九年级数学_223_实际问题与二次函数_课时同步检测 题型:解答题
已知:一个边长为
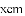
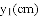 和面积增大的部分
和面积增大的部分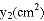 分别是
分别是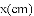
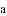
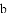
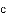
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期人教版九年级数学_223_实际问题与二次函数_课时同步检测 题型:解答题
如图,小明在一次高尔夫球争霸赛中从山坡上的点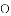
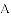
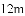
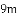
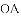
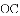
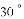 ,
,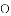
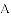
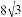
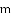
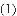
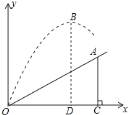
查看答案和解析>>
科目: 来源:2018-2019学年度第一学期人教版九年级数学_223_实际问题与二次函数_课时同步检测 题型:解答题
如图9,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(-2,0),B(-1, -3).
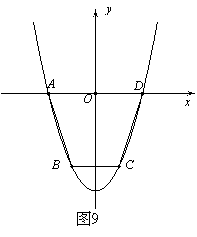
(1)求抛物线的解析式;(3分)
(2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标;(2分)
(3)在第(2)问的结论下,抛物线上的点P使S△PAD=4S△ABM成立,求点P坐标.(4分)
查看答案和解析>>
科目: 来源:2018年青岛版九年级上册数学第二章解直角三角形章末检测(一) 题型:单选题
如果把Rt△ABC的三边长度都扩大2倍,那么锐角A的四个三角比的值( )
A. 都扩大到原来的2倍 B. 都缩小到原来的 C. 都没有变化 D. 都不能确定
C. 都没有变化 D. 都不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com