如图，在中国象棋的残局上建立平面直角坐标系，如果“相”和“兵”的坐标分别是（3，﹣1）和（﹣3，1），那么“卒”的坐标为_____．

在平面直角坐标系中，O为坐标原点，点A(-a，a)(a>0)，点B(-a-4，a+3)，C为该直角坐标系内的一点，连结AB，OC．若AB∥OC且AB=OC，则点C的坐标为________

在平面直角坐标系中，将点（3，﹣2）先向右平移2个单位长度，再向上平移3个单位长度，则所得点的坐标是_____．

如图，△ABO中，AB⊥OB，OB=，AB=1，把△ABO绕点O逆时针旋转120°后得到△A1B1O，则点B1的坐标为_____．

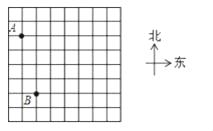
在一次夏令营活动中，老师将一份行动计划藏在没有任何标记的点C处，只告诉大家两个标志点A，B的坐标分别为（﹣3，1）、（﹣2，﹣3），以及点C的坐标为（3，2）（单位：km）．

（1）请在图中建立直角坐标系并确定点C的位置；

（2）若同学们打算从点B处直接赶往C处，请用方位角和距离描述点C相对于点B的位置．

如图，在平面直角坐标系中，线段AB的两个端点坐标分别为A（2，3），B（2，﹣1）．

（1）作出线段AB关于y轴对称的线段CD．

（2）怎样表示线段CD上任意一点P的坐标？

在平面直角坐标系中，已知A（﹣1，1），B（3，4），C（3，8）．

（1）建立平面直角坐标系，描出A、B、C三点，求出三角形ABC的面积；

（2）求出三角形ABO（若O是你所建立的坐标系的原点）的面积．

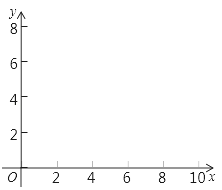
如图，在平面直角坐标系中，四边形ABCD各顶点的坐标分别是A（0，0），B（7，0），C（9，5），D（2，7）．

（1）在坐标系中，画出此四边形；

（2）求此四边形的面积．

在平面直角坐标系xOy中，对于点P（x，y），若点Q的坐标为（ax+y，x+ay），其中a为常数，则称点Q是点P的“a级关联点”．例如，点P（1，4）的“3级关联点”为Q（3×1+4，1+3×4），即Q（7，13）．

（1）已知点A（﹣2，6）的“级关联点”是点A1，点B的“2级关联点”是B1（3，3），求点A1和点B的坐标；

（2）已知点M（m﹣1，2m）的“﹣3级关联点”M′位于y轴上，求M′的坐标；

（3）已知点C（﹣1，3），D（4，3），点N（x，y）和它的“n级关联点”N′都位于线段CD上，请直接写出n的取值范围．

对于平面直角坐标系xOy中的点P（a，b），若点P′的坐标为（a+kb，ka+b）（其中k为常数，且k≠0），

则称点P′为点P的“k属派生点”．例如：P（1，4）的“2属派生点”为P′（1+2×4，2×1+4），即P′（9，6）．

（Ⅰ）点P（﹣2，3）的“3属派生点”P′的坐标为　 　；

（Ⅱ）若点P的“5属派生点”P′的坐标为（3，﹣9），求点P的坐标；

（Ⅲ）若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且线段PP′的长度为线段OP长度的2倍，求k的值．