如图，△ABC中，AB＝17，BC＝10，CA＝21，AM平分∠BAC，点D、E分别为AM、AB上的动点，则BD+DE的最小值是_____．

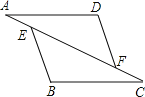
如图，点A、E、F、C在同一条直线上，AD∥BC，AD=CB，AE=CF．求证：BE=DF．

如图，在四边形ABCD中，AB＝AD，∠ABC＝∠ADC．求证：BC＝DC．

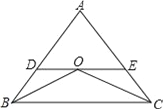
如图，已知OB、OC为△ABC的角平分线，DE∥BC，△ADE的周长为10，BC长为8，求△ABC的周长．

如图，某住宅小区在施工过程中留下了一块空地，已知AD=8米，CD=6米，∠ADC=90°，AB=26米，BC=24米，小区为美化环境，欲在空地上铺草坪，已知草坪每平方米100元，试问用该草坪铺满这块空地共需花费多少元？

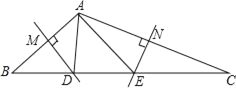
（10分）如图，△ABC中，边AB、AC的垂直平分线分别交BC于D、E．

（1）若BC=10，则△ADE周长是多少？为什么？

（2）若∠BAC=128°，则∠DAE的度数是多少？为什么？

如图，∠BAC的平分线与BC的垂直平分线DG相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F，AB=6，AC=3，求BE的长．

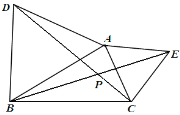
如图，已知△ABD和△AEC中，AD=AB，AE=AC，∠DAB=∠EAC=60°，CD、 BE相交于点P．

（1）用全等三角形判定方法证明：BE＝DC

（2）求∠BPC的度数；

（3）在（2）的基础上，经过深入探究后发现：射线AP平分∠BPC，请判断你的发现是否正确，并说明理由．

（1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．

下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．

证明：在边AB上截取AE=MC，连ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．

∴∠NMC=180°—∠AMN­—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE．

（下面请你完成余下的证明过程）

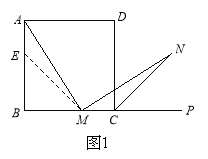
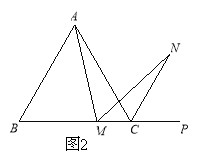
（2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．

（3）若将（1）中的“正方形ABCD”改为“正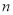边形ABCD……X”，请你作出猜想：当∠AMN= °时，结论AM=MN仍然成立．（直接写出答案，不需要证明）

问题背景：

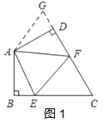
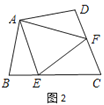
如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，EF分别是BC，CD上的点，且∠EAF＝60°，探究图中线段BE，EF，FD之间的数量关系.

小王同学探究此问题的方法是延长FD到点G，使DG＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是__________________；

探索延伸：

如图2，若在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E，F分别是BC，CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立，并说明理由；

结论应用：

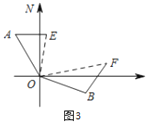
如图3，在某次军事演习中，舰艇甲在指挥中心(O处)北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等．接到行动指令后，舰艇甲向正东方向以50海里/小时的速度前进，舰艇乙沿北偏东50°的方向以60海里/小时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇与指挥中心O之间夹角∠EOF=70°，试求此时两舰艇之间的距离．

能力提高：

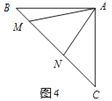
如图4，等腰直角三角形ABC中，∠BAC＝90°，AB＝AC，点M，N在边BC上，且∠MAN＝45°．若BM＝5，CN＝12，则MN的长为_________．（直接写出答案）