
科目: 来源:云南省数学学业水平考试 几何综合检测 题型:单选题
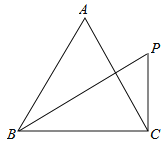
(4分)如图,在边长为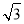 的等边三角形ABC中,过点C垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
的等边三角形ABC中,过点C垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
A.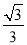 B.
B.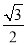 C.
C.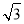 D.1
D.1
查看答案和解析>>
科目: 来源:云南省数学学业水平考试 几何综合检测 题型:单选题
如图,已知△ABC,AB=AC,将△ABC沿边BC翻转,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是( )
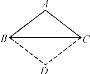
A. 四条边相等的四边形是菱形 B. 一组邻边相等的平行四边形是菱形
C. 对角线互相垂直的平行四边形是菱形 D. 对角线互相垂直平分的四边形是菱形
查看答案和解析>>
科目: 来源:云南省数学学业水平考试 几何综合检测 题型:解答题
如图,Rt△ABC中,∠C=90°,AB=14,AC=7,D是BC上一点,BD=8,DE⊥AB,垂足为E,求线段DE的长.
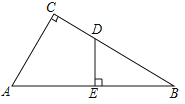
查看答案和解析>>
科目: 来源:云南省数学学业水平考试 几何综合检测 题型:解答题
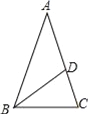
如图,在△ABC中,AB=AC=1,BC=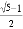 ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC•CD的大小关系;
(2)求∠ABD的度数.
查看答案和解析>>
科目: 来源:云南省数学学业水平考试 几何综合检测 题型:解答题
如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
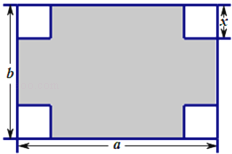
(1)用a,b,x表示纸片剩余部分的面积;
(2)当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.
查看答案和解析>>
科目: 来源:云南省数学学业水平考试 几何综合检测 题型:填空题
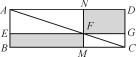
数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
(以上材料来源于《古证复原的原则》《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据上图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),
S矩形EBMF=S△ABC-(______________+______________).
易知,S△ADC=S△ABC,______________=______________,______________=______________.
可得S矩形NFGD=S矩形EBMF.
查看答案和解析>>
科目: 来源:云南省数学学业水平考试 几何综合检测 题型:解答题
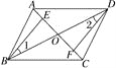
如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上.
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.
查看答案和解析>>
科目: 来源:云南省数学学业水平考试 几何综合检测 题型:解答题
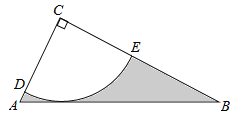
如图,Rt△ABC中,∠C=90°,AC=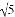 ,tanB=
,tanB= ,半径为2的⊙C,分别交AC,BC于点D,E,得到
,半径为2的⊙C,分别交AC,BC于点D,E,得到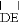 .
.
(1)求证:AB为⊙C的切线;
(2)求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com