
科目: 来源:重庆市江津区2018-2019学年八年级上学期七校联考数学试卷 题型:填空题
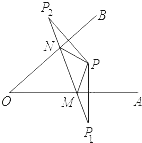
如图所示,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为_____.
查看答案和解析>>
科目: 来源:重庆市江津区2018-2019学年八年级上学期七校联考数学试卷 题型:填空题
下列图形是将等边三角形按一定规律排列,则第



查看答案和解析>>
科目: 来源:重庆市江津区2018-2019学年八年级上学期七校联考数学试卷 题型:解答题
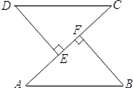
已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足AE=CF. 求证:DE=BF;
查看答案和解析>>
科目: 来源:重庆市江津区2018-2019学年八年级上学期七校联考数学试卷 题型:解答题
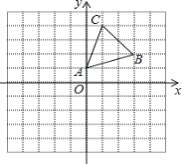
如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴对称的图形△A1B1C1;
(2)写出顶点A1,B1,C1的坐标;
(3)若正方形网格每两个格点间为一个单位长度,求△A1B1C1的面积.
查看答案和解析>>
科目: 来源:重庆市江津区2018-2019学年八年级上学期七校联考数学试卷 题型:解答题
如图所示,已知AC∥BD,EA,EB分别平分∠CAB和∠DBA,CD过E点.求证:AB=AC+BD.

查看答案和解析>>
科目: 来源:重庆市江津区2018-2019学年八年级上学期七校联考数学试卷 题型:解答题
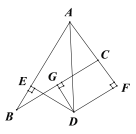
已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)试说明:BE=CF;(2)若AF=3,BC=4,求△ABC的周长.
查看答案和解析>>
科目: 来源:重庆市江津区2018-2019学年八年级上学期七校联考数学试卷 题型:解答题
阅读下列两则材料:
材料一:我们可以将任意三位数记为 (其中a,b,c分别表示该数百位数字、十位数字和个位数字,且a≠0),显然
(其中a,b,c分别表示该数百位数字、十位数字和个位数字,且a≠0),显然 =100a+10b+c.
=100a+10b+c.
材料二:若一个三位数的百位数字、十位数字和个位数字均不为0,则称之为原始数,比如123就是一个原始数,将原始数的三个数位上的数字交换顺序,可产生出5个原始数,比如由123可以产生出132,213,231,312,321这5个原始数.将这6个数相加,得到的和1332称为由原始数123生成的终止数.利用材料解决下列问题:
(1)分别求出由下列两个原始数生成的终止数:243,537;
(2)若一个原始数 的终止数是另一个原始数
的终止数是另一个原始数 的终止数的3倍,分别求出所有满足条件的这两个原始数.
的终止数的3倍,分别求出所有满足条件的这两个原始数.
查看答案和解析>>
科目: 来源:重庆市江津区2018-2019学年八年级上学期七校联考数学试卷 题型:解答题
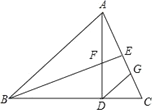
如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
求证:(1)∠BAD=2∠DAC (2)EF=EG.
查看答案和解析>>
科目: 来源:重庆市江津区2018-2019学年八年级上学期七校联考数学试卷 题型:解答题
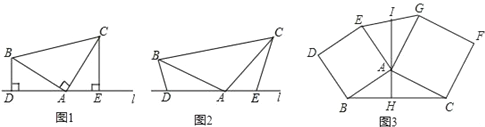
(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线L经过点A,BD⊥直线L,CE⊥直线L,垂足分别为点D、E.证明:DE=BD+CE.
(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线L上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图③,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高,延长HA交EG于点I,求证:I是EG的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com