
科目: 来源:贵州省黔南州2018届中考数学二模试卷 题型:填空题
如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是_____.
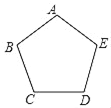
查看答案和解析>>
科目: 来源:贵州省黔南州2018届中考数学二模试卷 题型:填空题
如图是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为_米.(结果精确到0.1米,参考数据:  ≈1.41,
≈1.41,  ≈1.73)
≈1.73)

查看答案和解析>>
科目: 来源:贵州省黔南州2018届中考数学二模试卷 题型:填空题
瑞士的一位中学教师巴尔末从光谱数据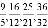 ,…中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第9个数_____.
,…中,成功地发现了其规律,从而得到了巴尔末公式,继而打开了光谱奥妙的大门.请你根据这个规律写出第9个数_____.
查看答案和解析>>
科目: 来源:贵州省黔南州2018届中考数学二模试卷 题型:解答题
为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60?x<70 | 17 | 0.17 |
B | 70?x<80 | 30 | a |
C | 80?x<90 | b | 0.45 |
D | 90?x<100 | 8 | 0.08 |
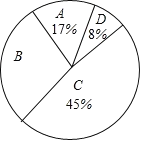
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
查看答案和解析>>
科目: 来源:贵州省黔南州2018届中考数学二模试卷 题型:解答题
自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如: ;
; <0等.那么如何求出它们的解集呢?
<0等.那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若a>0,b>0,则 >0;若a<0,b<0,则
>0;若a<0,b<0,则 >0;
>0;
(2)若a>0,b<0,则 <0;若a<0,b>0,则
<0;若a<0,b>0,则 <0.
<0.
反之:(1)若 >0,则
>0,则 或
或
(2)若 <0,则 或 .
<0,则 或 .
根据上述规律,求不等式 >0的解集.
>0的解集.
查看答案和解析>>
科目: 来源:贵州省黔南州2018届中考数学二模试卷 题型:解答题
如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
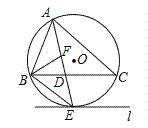
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目: 来源:贵州省黔南州2018届中考数学二模试卷 题型:解答题
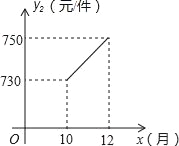
某企业为杭州计算机产业基地提供电脑配件.受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
价格y1(元/件) | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
随着国家调控措施的出台,原材料价格的涨势趋缓,10至12月每件配件的原材料价格y2(元)与月份x(10≤x≤12,且x取整数)之间存在如图所示的变化趋势:
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出y1 与x之间的函数关系式,根据如图所示的变化趋势,直接写出y2与x之间满足的一次函数关系式;
(2)若去年该配件每件的售价为1000元,生产每件配件的人力成本为50元,其它成本30元,该配件在1至9月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤9,且x取整数),10至12月的销售量p2(万件)p2=﹣0.1x+2.9(10≤x≤12,且x取整数).求去年哪个月销售该配件的利润最大,并求出这个最大利润.
查看答案和解析>>
科目: 来源:贵州省黔南州2018届中考数学二模试卷 题型:解答题
如图,已知抛物线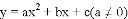 的对称轴为直线
的对称轴为直线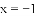
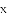
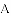
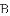
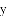
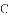
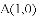
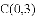
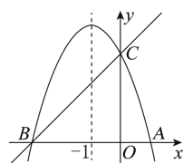
(1)若直线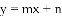
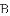
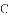
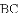
(2)在抛物线的对称轴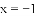
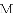
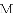
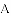
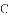
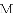
(3)设点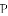
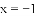
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com